
【题目】已知![]() ,
,![]() 为椭圆E:
为椭圆E:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 的直线l与椭圆E有且只有一个交点T.
的直线l与椭圆E有且只有一个交点T.
(1)求![]() 面积的取值范围.
面积的取值范围.
(2)若有一束光线从点![]() 射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
【答案】(1)![]() ;(2)是,定点
;(2)是,定点![]()
【解析】
(1)由题意设直线l的方程为:![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,由
,由![]() ,解得
,解得![]() ,由韦达定理得切点T的
,由韦达定理得切点T的 ,
,![]() 的面积
的面积![]() ,根据m的范围即可求出;
,根据m的范围即可求出;
(2)由对称性和(1)得,不妨取切点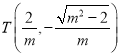 ,则直线l:
,则直线l:![]() ,设
,设![]() 关于l对称的点为
关于l对称的点为![]() ,经计算得
,经计算得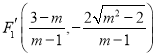 ,
,![]() ,直线
,直线![]()
![]() 恒过定点
恒过定点![]() ,即可得答案.
,即可得答案.
(1)![]() ,∴直线l的斜率存在且不为0,故设直线l的方程为l:
,∴直线l的斜率存在且不为0,故设直线l的方程为l:![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
因为直线l与椭圆E有且只有一个交点T,所以![]() ,解得
,解得![]() ,
,
此时求得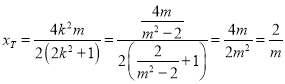 ,由
,由![]() ,得
,得![]() ,
,
![]() ,所以切点T的坐标为
,所以切点T的坐标为 ,又
,又![]() ,
,![]() ,
,
所以![]() 的面积
的面积![]() ,又
,又![]() ,
,![]() ,
,![]() .
.
(2)由对称性和(1)得,不妨取切点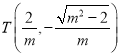 ,则直线l:
,则直线l:![]() ,设
,设![]() 关于l对称的点为
关于l对称的点为![]() ,
,
则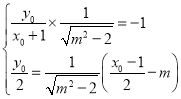 ,
,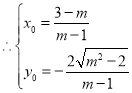 ,
,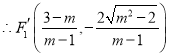 .
.
![]() ,
,![]() ,
,
故直线![]() 的斜率为
的斜率为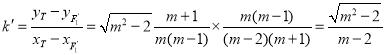 ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() 恒过定点
恒过定点![]() ,
,
所以光线![]() 被直线l反射后恒过定点
被直线l反射后恒过定点![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由!
的取值范围;若不存在,请说明理由!
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,在以坐标原点为极点,
,在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从洛阳的高中生中,随机抽取了55人,从上海的高中生中随机抽取了45人进行答题.洛阳高中生答题情况是:选择家的占![]() 、选择朋友聚集的地方的占
、选择朋友聚集的地方的占![]() 、选择个人空间的占
、选择个人空间的占![]() .上海高中生答题情况是:选择朋友聚集的地方的占
.上海高中生答题情况是:选择朋友聚集的地方的占![]() 、选择家的占
、选择家的占![]() 、选择个人空间的占
、选择个人空间的占![]() .
.
(1)请根据以上调查结果将下面![]() 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有![]() 的把握认为“恋家(在家里感到最幸福)”与城市有关:
的把握认为“恋家(在家里感到最幸福)”与城市有关:
在家里最幸福 | 在其它场所最幸福 | 合计 | |
洛阳高中生 | |||
上海高中生 | |||
合计 |
(2) 从被调查的不“恋家”的上海学生中,用分层抽样的方法选出4人接受进一步调查,从被选出的4 人中随机抽取2人到洛阳交流学习,求这2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() d.
d.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼.太极图展现了一种相互转化,相对统一的和谐美.定义:能够将圆![]() 的周长和面积同时等分成两个部分的函数称为圆
的周长和面积同时等分成两个部分的函数称为圆![]() 的一个“太极函数”.现有下列说法:①对于圆
的一个“太极函数”.现有下列说法:①对于圆![]() :
:![]() 的所有非常数函数的太极函数中,一定不能为偶函数;②函数
的所有非常数函数的太极函数中,一定不能为偶函数;②函数![]() 是圆
是圆![]() :
:![]() 的一个太极函数;③存在圆
的一个太极函数;③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的一个太极函数;④直线
的一个太极函数;④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() :
:![]() (
(![]() )的太极函数;⑤若函数
)的太极函数;⑤若函数![]() (
(![]() )是圆
)是圆![]() :
:![]() 的太极函数,则
的太极函数,则![]() .其中正确的是__________.
.其中正确的是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com