
分析 令t(x)=6+x-x2≥0,求得-2≤x≤3且f(x)=$\sqrt{t(x)}$,本题即求函数t(x)在[-2,3]上的减区间;再利用二次函数的性质可得t(x)在[-2,3]上的减区间.
解答 解:令t(x)=6+x-x2≥0,求得-2≤x≤3,故函数f(x)的定义域为[-2,3],且f(x)=$\sqrt{t(x)}$,
故本题即求函数t(x)在[-2,3]上的减区间.
再利用二次函数的性质可得t(x)在[-2,3]上的减区间为[$\frac{1}{2}$,3],
故答案为[$\frac{1}{2}$,3].
点评 本题主要考查二次函数的性质,复合函数的单调性,体现了转化的数学思想,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
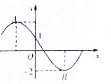 如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )
如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )| A. | -1 | B. | 2 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{3},1)∪(\sqrt{3},+∞)$ | B. | $(-∞,-1)∪(\sqrt{3},+∞)$ | C. | $(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$ | D. | $(-\sqrt{3},-1)∪(1,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com