
分析 由题意将条件转化为:方程xex=a在R上有两个不同的实数根,设g(x)=xex并求出g′(x),由导数与函数单调性的关系,判断出g(x)在定义域上的单调性,求出g(x)的最小值,结合g(x)的单调性、最值、函数值的范围画出大致的图象,由图象求出实数a的取值范围.
解答 解:由题意知:若f(x)具有性质P,
则在定义域内xf(x)=1有两个不同的实数根,
∵$f(x)=\frac{{e}^{x}}{a}$,∴$x•\frac{{e}^{x}}{a}=1$,
即方程xex=a在R上有两个不同的实数根,
设g(x)=xex,则g′(x)=ex+xex=(1+x)ex,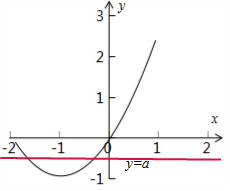
由g′(x)=0得,x=-1,
∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,
∴当x=-1时,g(x)取到最小值是g(-1)=$-\frac{1}{e}$,
∵x<0,g(x)<0、x>0,g(x)>0,
∴当方程xex=a在R上有两个不同的实数根时,
即函数g(x)与y=a的图象有两个交点,
由图得$-\frac{1}{e}<a<0$,
∴实数a的取值范围为$(-\frac{1}{e},0)$,
故答案为:$(-\frac{1}{e},0)$.
点评 本题是新定义题,考查导数与函数单调性的关系,方程根的问题转化为函数图象的交点问题,以及转化思想,数形结合思想,考查分析问题、解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
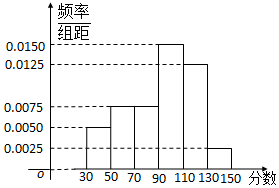 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com