
分析 双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)可得A、F、B1和B2各点的坐标,B2F⊥AB1,利用向量数量积的坐标公式得到ac-b2=0,结合b2=c2-a2和离心率公式,化简得离心率e的方程,即可解出该双曲线的离心率.
解答 解:由题意,双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)可得A(a,0),F(c,0),B1(0,b),B2(0,-b)
∵$\overrightarrow{A{B}_{1}}$=(-a,b),$\overrightarrow{{B}_{2}F}$=(c,b)
∴由$\overrightarrow{A{B}_{1}}$⊥$\overrightarrow{{B}_{2}F}$得$\overrightarrow{A{B}_{1}}$•$\overrightarrow{{B}_{2}F}$=0,即-ac+b2=0
可得b2=ac,即c2-ac-a2=0,两边都除以a2可得e2-e-1=0
解之得e=$\frac{\sqrt{5}+1}{2}$(舍负)
故答案为:$\frac{\sqrt{5}+1}{2}$.
点评 本题给出双曲线方程,在已知向量垂直的情况下求离心率.着重考查了平面向量数量积公式和双曲线的标准方程与简单几何性质等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}-\sqrt{2}$ | B. | $3+\frac{{\sqrt{2}}}{2}$ | C. | $\frac{3}{2}+\sqrt{2}$ | D. | $3-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$6-2\sqrt{3}$) | B. | (2,$\sqrt{3}+1$) | C. | (4,$8-2\sqrt{3}$) | D. | (0,$4-2\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年浙江普通高校招生学业水平考试数学试卷(解析版) 题型:选择题
如图,设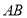 为圆锥
为圆锥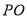 的底面直径,
的底面直径,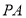 为母线,点
为母线,点 在底面圆周上,若
在底面圆周上,若 ,
,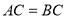 ,则二面角
,则二面角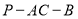 大小的正切值是( )
大小的正切值是( )

A.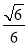 B.
B. C.
C.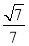 D.
D.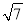
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com