
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
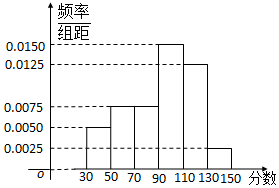 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
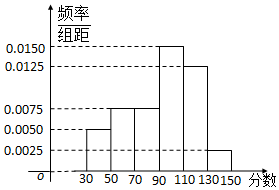 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源:2016-2017学年浙江普通高校招生学业水平考试数学试卷(解析版) 题型:解答题
设函数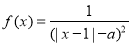 的定义域为
的定义域为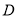 ,其中
,其中 .
.
(1)当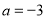 时,写出函数
时,写出函数 的单调区间(不要求证明);
的单调区间(不要求证明);
(2)若对于任意的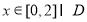 ,均有
,均有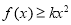 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(理)试卷(解析版) 题型:选择题
已知 满足约束条件
满足约束条件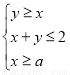 ,且
,且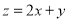 的最大值是最小值的3倍,则
的最大值是最小值的3倍,则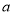 的值是( )
的值是( )
A. B.
B.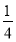
C.7 D.不存在
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com