
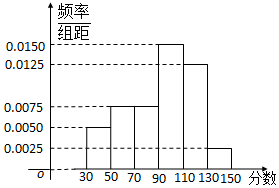
 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:分析 (1)由频率分布直方图计算数据的平均分;
(2)计算样本中分数在[30,50)和[130,150]的人数,根据分层抽样原理求出抽取的人数;
(3)计算抽取的6人中分数在[130,150]的人数,求出ξ的所有取值与概率分布,计算数学期望值.
解答 解:(1)由频率分布直方图,得
该校高三学生本次数学考试的平均分为
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100
+0.0125×20×120+0.0025×20×140=92;…(4分)
(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人,
所以抽取的6人中分数在[130,150]的人有$3×\frac{6}{9}=2$(人);…(8分)
(3)由(2)知:抽取的6人中分数在[130,150]的人有2人,
依题意ξ的所有取值为0、1、2,
当ξ=0时,$P(ξ=0)=\frac{C_4^3}{C_6^3}=\frac{1}{5}$;
当ξ=1时,$P(ξ=1)=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$;
当ξ=2时,$P(ξ=2)=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$;
∴$E(ξ)=0×\frac{1}{5}+1×\frac{3}{5}+2×\frac{1}{5}=1$.…(12分)
点评 本题主要考查了频率分布直方图以及平均数和概率的计算问题,也考查了运用统计知识解决简单实际问题的能力,是基础题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
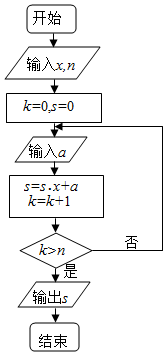 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )
秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(理)试卷(解析版) 题型:选择题
已知集合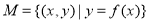 ,若对于任意
,若对于任意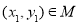 ,存在
,存在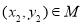 ,使得
,使得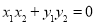 成立,则称集合
成立,则称集合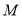 是“理想集合”.给出下列5个集合:
是“理想集合”.给出下列5个集合:
①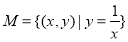 ;
;
②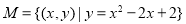 ;
;
③ ;
;
④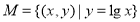 ;
;
⑤ .
.
其中所有“理想集合”的序号是( )
A.①② B.③⑤ C.②③⑤ D.③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com