
分析 (1)由已知可得:a1=3,${a}_{n}=\sqrt{{a}_{n-1}^{2}+n}$,平方可得:${a}_{n}^{2}$-${a}_{n-1}^{2}$=n.利用累加求和方法、等差数列的求和公式即可得出.
(2)由a1=3,an=$\sqrt{{a}_{n-1}+2}$,可得a2=$\sqrt{5}$,a3=$\sqrt{\sqrt{5}+2}$.由an=$\sqrt{{a}_{n-1}+2}$>0,两边平方可得:${a}_{n}^{2}={a}_{n-1}$+2,于是${a}_{n+1}^{2}={a}_{n}$+2.相减可得:(an+1+an)(an+1-an)=an-an-1,由an>0,可得an+1-an与an-an-1同号,即可得出.
(3)由(2)可得:${a}_{n+1}^{2}={a}_{n}$+2,${a}_{n+1}^{2}-4$=an-2,因式分解为:(an+1+2)(an+1-2)=an-2,可知:an+1-2与an-2同号,可得:an-2>0,$\frac{1}{{a}_{n}+2}$<$\frac{1}{4}$,因此an+1-2$<\frac{1}{4}$(an-2),由n≥2时,(an+2)(an-2)=an-1-2,可得bn=an+2=$\frac{{a}_{n-1}-2}{{a}_{n}-2}$.可得b2b3…bn=$\frac{{a}_{1}-2}{{a}_{n}-2}$=$\frac{1}{{a}_{n}-2}$.由an+1-2$<\frac{1}{4}$(an-2),n≥2时,可得:|an-2|<$\frac{1}{4}$|an-1-2|<…<$\frac{1}{{4}^{n-1}}|{a}_{1}-2|$=$\frac{1}{{4}^{n-1}}$.$\frac{1}{{a}_{n}-2}$>4n-1,进而判断出结论.
解答 解:(1)由已知可得:a1=3,${a}_{n}=\sqrt{{a}_{n-1}^{2}+n}$,平方可得:${a}_{n}^{2}$-${a}_{n-1}^{2}$=n.
∴${a}_{n}^{2}$=(${a}_{n}^{2}$-${a}_{n-1}^{2}$)+$({a}_{n-1}^{2}-{a}_{n-2}^{2})$+…+$({a}_{2}^{2}-{a}_{1}^{2})$+${a}_{1}^{2}$=n+(n-1)+…+2+9=$\frac{n(n+1)}{2}$+8.
∴an=$\sqrt{\frac{{n}^{2}+n+16}{2}}$.
(2)由a1=3,an=$\sqrt{{a}_{n-1}+2}$,可得a2=$\sqrt{5}$,a3=$\sqrt{\sqrt{5}+2}$.
由an=$\sqrt{{a}_{n-1}+2}$>0,两边平方可得:${a}_{n}^{2}={a}_{n-1}$+2,于是${a}_{n+1}^{2}={a}_{n}$+2.
相减可得:(an+1+an)(an+1-an)=an-an-1,
∵an>0,∴an+1-an与an-an-1同号,∵a2-a1=$\sqrt{5}$-3<0,
∴an+1-an<0,即an+1<an,
∴数列{an} 单调递减.
(3)由(2)可得:${a}_{n+1}^{2}={a}_{n}$+2,∴${a}_{n+1}^{2}-4$=an-2,因式分解为:(an+1+2)(an+1-2)=an-2,
可知:an+1-2与an-2同号,由a1-2=3-2=1>0,可得:an-2>0,即an+2>4,∴$\frac{1}{{a}_{n}+2}$<$\frac{1}{4}$,
∴an+1-2$<\frac{1}{4}$(an-2),∵n≥2时,(an+2)(an-2)=an-1-2,∴bn=an+2=$\frac{{a}_{n-1}-2}{{a}_{n}-2}$.
则b2b3…bn=$\frac{{a}_{1}-2}{{a}_{2}-2}$•$\frac{{a}_{2}-2}{{a}_{3}-2}$•…•$\frac{{a}_{n-1}-2}{{a}_{n}-2}$=$\frac{{a}_{1}-2}{{a}_{n}-2}$=$\frac{1}{{a}_{n}-2}$.由an+1-2$<\frac{1}{4}$(an-2),n≥2时,
可知:|an-2|<$\frac{1}{4}$|an-1-2|$<\frac{1}{{4}^{2}}$|an-2-2|<…<$\frac{1}{{4}^{n-1}}|{a}_{1}-2|$=$\frac{1}{{4}^{n-1}}$.
∴$\frac{1}{{a}_{n}-2}$>4n-1,若存在常数M,对任意n≥2,有b2b3…bn≤M.则M>0,4n-1≤M,而当n>$[\frac{lnM}{ln4}]$+2时,有4n-1≥M恒成立,故不存在常数M,对任意n≥2,有b2b3…bn≤M.
点评 本题考查了等比数列的通项公式与求和公式、数列递推关系、不等式的性质与解法、放缩法、累加求和方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{4}π$ | B. | $\frac{9}{4}π$ | C. | $\frac{5}{4}π$ | D. | $\frac{7}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD,SA⊥平面ABCD,E是SC的中点,AD=AB=2,CD=CB=2$\sqrt{3}$,AC=4,SA=2$\sqrt{2}$.
如图,四棱锥S-ABCD,SA⊥平面ABCD,E是SC的中点,AD=AB=2,CD=CB=2$\sqrt{3}$,AC=4,SA=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5}{12}$π],(k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],(k∈Z) | ||
| C. | [kπ+$\frac{5}{12}$π,kπ+$\frac{11}{12}$π],(k∈Z) | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2}{3}$π],(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{2}{9}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
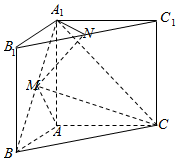 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com