
已知抛物线y2=4x的焦点为F,准线为l,l与双曲线 -y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
-y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
(A) (B)
(B) (C)2 (D)
(C)2 (D)  +1
+1
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
已知△ABC外接圆半径R= ,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
(A)  -
- =1 (B)
=1 (B)  -
- =1
=1
(C) 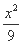 -
- 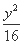 =1 (D)
=1 (D) 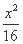 -
-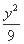 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,中心均为原点O的双曲线与椭圆有公共焦点,M、N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是( )
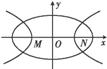
(A)3 (B)2 (C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
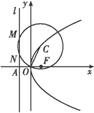
(1)若点C的纵坐标为2,求|MN|;
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
某校要从高一、高二、高三共2 012名学生中选取50名组成志愿团,若采用下面的方法选取,先用简单随机抽样的方法从2 012人中剔除12人,剩下的2 000人再按分层抽样的方法进行,则每人入选的概率( )
A.都相等且为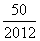 B.都相等且为
B.都相等且为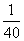
C.不会相等 D.均不相等
查看答案和解析>>
科目:高中数学 来源: 题型:
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) | [80,85) | [80,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com