
分析 (1)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数的极值即可;
(2)求出f(x)的最大值,问题转化为g(x)min≥1,根据函数的单调性求出m的范围即可.
解答 解:(1)$g'(x)=\frac{{({x-m})({x-1})}}{x^2}({x>0})$-----------------(2分)
①当m≤0时,f(x)在区间(0,1)上是减函数,在区间(1,+∞)上是增函数,
∴f(x)极小值=f(1)=1-m,无极大值.----------------------(3分)
②当0<m<1时,f(x)在区间(0,m)上是增函数,
在区间(m,1)上是减函数,在区间(1,+∞)上是增函数,
∴f(x)极大值=f(m)=m-(m+1)lnm-1,f(x)极小值=f(1)=1-m.--------(4分)
③当m=1时,f(x)在区间(0,+∞)是增函数,∴f(x)无极值.----------------(5分)
④当m>1时,f(x)在区间(0,1)上是增函数,
在区间(1,m)上是减函数,在区间(m,+∞)上是增函数,
∴f(x)极小值=f(m)=m-(m+1)lnm-1,f(x)极大值=f(1)=1-m.---------(6分)
(2)∵$f(x)=-{(x-\frac{3}{2})^2}+2$,∴$f{(x)_{max}}=f(\frac{3}{2})=2$,
由题意,当x∈[1,e]时,f(x)max-g(x)min≤1即g(x)min≥1.---------------(8分)
①当m≤1时,g(x)min=g(1)=1-m,∵1-m≥1,∴m≤0.----------------(10分)
②当1<m<e时,g(x)min=g(m)=m-(m+1)lnm-1,
令F(m)=m-(m+1)lnm-1(1<m<e),
则$F'(m)=-1-\frac{1}{m}<0$,∴F(m)是减函数,
∴F(m)<F(1)=0,∴g(m)<0,不合题意.-----------------(13分)
③当m≥e时,$g{(x)_{min}}=g(e)=e-(m+1)-\frac{m}{e}$,
∵$e-(m+1)-\frac{m}{e}≥1$,∴$m≤\frac{{{e^2}-2e}}{e+1}$,这与m≥e矛盾,舍去.-----------------------------(15分)
综上,m的取值范围是(-∞,0].--------------------------------(16分)
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
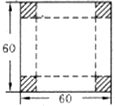 如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.
如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | ||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90 ) | 4 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={0,2},B={0,1},f:x→y=$\frac{x}{2}$ | |
| B. | A={-1,-2,-3,1,2},B={1,4},f:x→y=x2,x∈A,y∈B | |
| C. | A=R,B={y|y>0},f:x→y=$\frac{1}{{x}^{2}}$ | |
| D. | A=Z,B=N*,f:x→y=|x|,x∈A,y∈B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 旋钮所指刻度 | 起止时间 | 燃气表读数(m3) | ||
| 始 | 终 | 始 | 终 | |
| 5 | 0 | 8′07.60″ | 7.266 | 7.310 |
| 4 | 0 | 8′39.82″ | 7.310 | 7.347 |
| 3 | 0 | 9′54.35″ | 7.347 | 7.390 |
| 2 | 0 | 12′13.22″ | 7.390 | 7.451 |
| 旋钮所指刻度 | 耗气量(单位:L) | 时间(单位:s) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com