
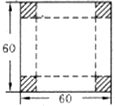
 如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.
如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
分析 先设箱底边长为xcm,则箱高h=$\frac{60-x}{2}$cm,得箱子容积,再利用导数的方法解决,应注意函数的定义域.
解答 解:设箱底边长为xcm,则箱高h=$\frac{60-x}{2}$cm,得箱子容积V=$\frac{60{x}^{2}-{x}^{3}}{2}$(0<x<60).
V′=60x-$\frac{3{x}^{2}}{2}$(0<x<60)
令V′=60x-$\frac{3{x}^{2}}{2}$=0,
解得 x=0(舍去),x=40,
∵x∈(0,40)时,V′(x)>0;x∈(40,60)时,V′(x)<0
∴V(x)在区间(0,40)上为增函数,区间(40,60)上为减函数
由此可得V(x)的最大值是V(40)=16000cm3.
故选D.
点评 本题以一个实际问题为例,求箱子的容积最大值.着重考查了函数模型及其应用和利用导数研究函数的单调性、求最值等知识,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2)(4) | B. | (1)(3) | C. | (2)(4) | D. | (1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
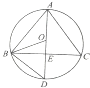 如图所示,D为△ABC的外接圆$\widehat{BC}$的中点,点O在AD上,且OD=BD,AD与BC相交于E.
如图所示,D为△ABC的外接圆$\widehat{BC}$的中点,点O在AD上,且OD=BD,AD与BC相交于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
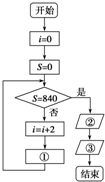
| A. | S=i(i+2),输出i,输出i-2 | B. | S=i2+2,输出i+2,输出i-2 | ||
| C. | S=i(i+2),输出i,输出i+2 | D. | S=i2+2,输出i,输出i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com