
| A. | S=i(i+2),输出i,输出i-2 | B. | S=i2+2,输出i+2,输出i-2 | ||
| C. | S=i(i+2),输出i,输出i+2 | D. | S=i2+2,输出i,输出i+2 |
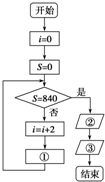
分析 框图执行的是找出乘积为840的两个相邻偶数,首先给两个变量i和S分别赋值0、0,在第一次执行完用0+2替换i后,应该算出前两个偶数的乘积,用得到的两个偶数的乘积替换S,然后判断S的是否满足等于840,若满足,则跳出循环,输出i与i+2,不满足,继续执行循环体,由此可以断定填充框图中①、②、③处语句.
解答 解:模拟程序的运行,可得
赋值i=0,S=0.
不满足条件S=840,执行循环体,i=0+2=2,S=2×4=8;
不满足条件S=840,执行循环体,i=2+2=4,S=4×6=24;
不满足条件S=840,执行循环体,i=4+2=6,S=6×8=48;
不满足条件S=840,执行循环体,i=6+2=8,S=8×10=80;
…
不满足条件S=840,执行循环体,i=26+2=28,S=28×30=840;
判断28×30=840,满足条件,跳出循环,输出28,输出30.
由以上运行步骤看出,填充框图中①、②、③处的语句分别是s=i*(i+2)、输出i、输出i+2.
故选:C.
点评 本题考查了循环结构中的当型循环,当型循环是先判断,后循环,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
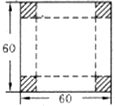 如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.
如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90 ) | 4 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={0,2},B={0,1},f:x→y=$\frac{x}{2}$ | |
| B. | A={-1,-2,-3,1,2},B={1,4},f:x→y=x2,x∈A,y∈B | |
| C. | A=R,B={y|y>0},f:x→y=$\frac{1}{{x}^{2}}$ | |
| D. | A=Z,B=N*,f:x→y=|x|,x∈A,y∈B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
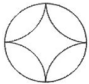 把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为$\frac{4}{π}-1$.
把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为$\frac{4}{π}-1$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值3,最小值-1 | B. | 有最大值 $2-\sqrt{7}$,无最小值 | ||
| C. | 有最大值 $7-2\sqrt{7}$,无最小值 | D. | 无最大值,也无最小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com