
| A. | 有最大值3,最小值-1 | B. | 有最大值 $2-\sqrt{7}$,无最小值 | ||
| C. | 有最大值 $7-2\sqrt{7}$,无最小值 | D. | 无最大值,也无最小值 |
分析 在同一坐标系中先画出f(x)与g(x)的图象,然后根据定义画出F(x),就容易看出F(x)有最大值,无最小值,解出两个函数的交点,即可求得最大值.
解答 解:在同一坐标系中先画出f(x)与g(x)的图象,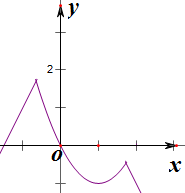
当f(x)<g(x)时,F(x)=f(x),表示f(x)的图象在g(x)的图象下方就去f(x)的图象,然后根据定义画出F(x),就容易看出F(x)有最大值,无最小值
当x<0时,由$\left\{\begin{array}{l}{f(x)=3+2x}\\{g(x)={x}^{2}-2x}\end{array}\right.$得x=2+$\sqrt{7}$(舍)或x=2-$\sqrt{7}$
此时F(x)的最大值为:7-2$\sqrt{7}$,
故选:C.
点评 此题考查阅读能力和函数图象的画法,必须弄懂F(x)是什么.先画出f(x)及g(x)与F(x)的图象.再比较f(x)与g(x)的大小,然后确定F(x)的图象.这是一道创新性较强的试题,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1)(2)(4) | B. | (1)(3) | C. | (2)(4) | D. | (1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
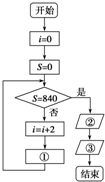
| A. | S=i(i+2),输出i,输出i-2 | B. | S=i2+2,输出i+2,输出i-2 | ||
| C. | S=i(i+2),输出i,输出i+2 | D. | S=i2+2,输出i,输出i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
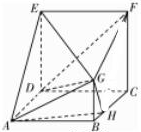 在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [2,+∞) | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在a∈R,使f (x)是偶函数 | |
| B. | 存在a∈R,f (x)是奇函数 | |
| C. | 对于任意的a∈R,f (x)在(0,+∞)上是增函数 | |
| D. | 对于任意的a∈R,f (x)在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-1,2) | C. | (1,-2) | D. | (2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com