
分析 由题意符合要求的四位偶数可分为三类:0在个位,2在个位,4在个位,对每一类分别计数再求它们的和即可得到无重复数字的四位偶数的个数.
解答 解:符合要求的四位偶数可分为三类:
第一类:0在个位时有$A_5^3$个;
第二类:2在个位时,首位从1,3,4,5中选定1个(有$A_4^1$种),十位和百位从余下的数字中选(有$A_4^2$种),于是有$A_4^1\cdotA_4^2$个;
第三类:4在个位时,与第二类同理,也有$A_4^1\cdotA_4^2$个.
由分类加法计数原理知,共有四位偶数:$A_5^3+A_4^1\cdotA_4^2+A_4^1\cdotA_4^2=156$个.
点评 本题考查分类计数及简单计数问题,解题的关键是理解所研究的事件,对计数问题分类计数,本题考查了分类讨论的思想,以及运用排列组合数公式进行计算的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
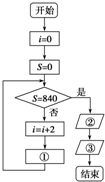
| A. | S=i(i+2),输出i,输出i-2 | B. | S=i2+2,输出i+2,输出i-2 | ||
| C. | S=i(i+2),输出i,输出i+2 | D. | S=i2+2,输出i,输出i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在a∈R,使f (x)是偶函数 | |
| B. | 存在a∈R,f (x)是奇函数 | |
| C. | 对于任意的a∈R,f (x)在(0,+∞)上是增函数 | |
| D. | 对于任意的a∈R,f (x)在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 这样的β只能作一个 | B. | 这样的β至多有一个 | ||
| C. | 这样的β至少可作一个 | D. | 这样的β不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-1,2) | C. | (1,-2) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com