
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90 ) | 4 | 0.1 |
分析 (1)利用频率分配表,直接求解众数和中位数.
(2)利用中位数与频率求出该居民区PM2.5年平均浓度,判断即可.
(3)随机变量ξ的可能取值为0,1,2.求出概率,得到分布列,然后求解期望与方差即可.
解答 解:(1)众数为22.5微克/立方米,中位数为37.5微克/立方米. …(4分)
(2)去年该居民区PM2.5年平均浓度为7.5×0.1+22.5×0.3+37.5×0.2+52.5×0.2+67.5×0.1+82.5×0.1=40.5(微克/立方米).因为40.5>35,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,
故该居民区的环境需要改进. …(7分)
(3)记事件A表示“一天PM2.5的24小时平均浓度符合环境空气质量标准”,
则$P(A)=\frac{9}{10}$.随机变量ξ的可能取值为0,1,2.且ξ~B$(2,\frac{9}{10})$
所以$P(ξ=k)=C_2^k{(\frac{9}{10})^k}{(1-\frac{9}{10})^{2-k}}(k=0,1,2)$,所以变量ξ的分布列为
| ξ | 0 | 1 | 2 |
| p | $\frac{1}{100}$ | $\frac{18}{100}$ | $\frac{81}{100}$ |
点评 本题考查频率分布表,独立重复试验的概率分布列以及期望与方差的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (1)(2)(4) | B. | (1)(3) | C. | (2)(4) | D. | (1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
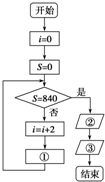
| A. | S=i(i+2),输出i,输出i-2 | B. | S=i2+2,输出i+2,输出i-2 | ||
| C. | S=i(i+2),输出i,输出i+2 | D. | S=i2+2,输出i,输出i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在a∈R,使f (x)是偶函数 | |
| B. | 存在a∈R,f (x)是奇函数 | |
| C. | 对于任意的a∈R,f (x)在(0,+∞)上是增函数 | |
| D. | 对于任意的a∈R,f (x)在(0,+∞)上是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com