
分析 此题首先需要由实际问题向数学问题转化,设设池底宽分别为a,高为h(h≥3m),成本为y,建立函数关系式,然后利用基本不等式求出最值即可求出所求.
解答 解:设池底宽分别为a,高为h(h≥3m),成本为y,
则∵长方形容器的容器为8m3,底部矩形长为2m,
∴2ah=8,∴ah=4.
∵该容器的底面造价是每平方米40元,侧面造价是每平方米20元,
y=2a•40+20[2(a+2)h]=80(a+h)+160=80($\frac{4}{h}$+h)+160,
∵h≥3,∴$\frac{4}{h}$+h≥$\frac{13}{3}$
故当h=3m,a=$\frac{4}{3}$m时,y取最小值$\frac{1520}{3}$元,
当容器底面池底宽为$\frac{4}{3}$m时,使得容器总造价最低,最小值为$\frac{1520}{3}$元.
点评 本题以棱柱的体积为载体,考查了基本不等式,难度不大,属于中档题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 0 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
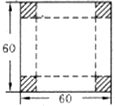 如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.
如图,在边长为60cm的正方形的四个角除去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长( )时,箱子容积最大.| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com