
 .
. .的单调区间;
.的单调区间; 的极值.
的极值.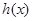 的单调增区间为
的单调增区间为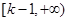 ,单调减区间为
,单调减区间为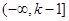
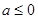 时,
时,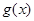 无极值;当
无极值;当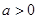 ,
,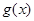 在
在 处取得极小值
处取得极小值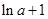 ,无极大值。
,无极大值。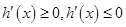 不等式即可;
不等式即可; ,在求极值时要对参数
,在求极值时要对参数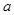 讨论,显然当
讨论,显然当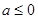 时
时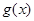 为增函数,无极值,当
为增函数,无极值,当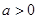 时可求得
时可求得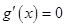 的根,再讨论两侧的单调性;判断极值的方法是先求得
的根,再讨论两侧的单调性;判断极值的方法是先求得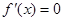 的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.
的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.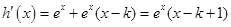
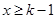 时,
时, 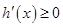 ,
,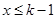 时,
时, 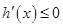 ,
,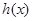 的单调增区间为
的单调增区间为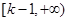 ,单调减区间为
,单调减区间为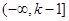 .
.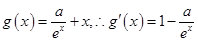
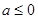 时,
时,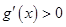 ,
,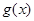 为
为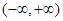 上的增函数,所以
上的增函数,所以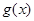 无极值。
无极值。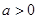 时,令
时,令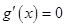 得,
得,
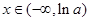 ,
,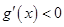 ;
;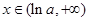 ,
,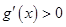
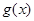 在
在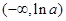 上单调递减,在
上单调递减,在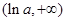 上单调递增
上单调递增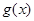 在
在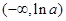 处取得极小值,且极小值为
处取得极小值,且极小值为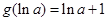 ,无极大值
,无极大值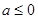 时,
时,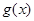 无极值;当
无极值;当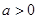 ,
,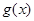 在
在 处取得极小值
处取得极小值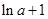 ,无极大值。
,无极大值。

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
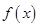 的定义域为
的定义域为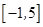 ,部分对应值如下表,
,部分对应值如下表,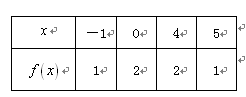
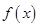 的导函数
的导函数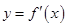 的图象如图所示.
的图象如图所示. 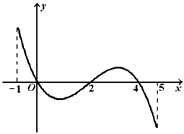
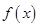 的命题:
的命题: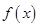 的极大值点为
的极大值点为 ,
,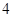 ;
;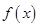 在
在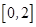 上是减函数;
上是减函数;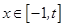 时,
时,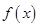 的最大值是2,那么
的最大值是2,那么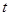 的最大值为4;
的最大值为4;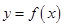 最多有2个零点.
最多有2个零点.| A.①② | B.③④ | C.①②④ | D.②③④. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com