
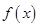 的定义域为
的定义域为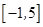 ,部分对应值如下表,
,部分对应值如下表,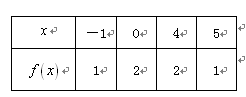
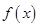 的导函数
的导函数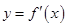 的图象如图所示.
的图象如图所示. 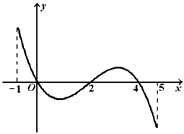
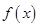 的命题:
的命题: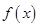 的极大值点为
的极大值点为 ,
, ;
;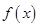 在
在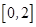 上是减函数;
上是减函数;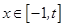 时,
时,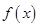 的最大值是2,那么
的最大值是2,那么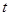 的最大值为4;
的最大值为4;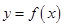 最多有2个零点.
最多有2个零点.| A.①② | B.③④ | C.①②④ | D.②③④. |
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:不详 题型:解答题
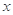 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为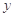 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用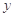 随每年改造生态环境总费用
随每年改造生态环境总费用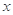 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少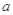 亿元,至多
亿元,至多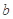 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用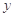 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用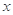 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用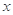 的25%.
的25%.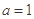 ,
,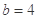 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=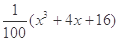 作为生态环境改造投资方案.
作为生态环境改造投资方案.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com