练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．若2x+4y=8，则x+2y的最大值是4．

    分析 利用基本不等式的性质、指数运算性质即可得出．

    解答 解：∵8=2x+4y=2x+22y≥2$\sqrt{{2}^{x}•{2}^{2y}}$，则x+2y≤4，当且仅当x=2y=2时取等号．
    故答案为：4．

    点评 本题考查了基本不等式的性质、指数运算性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届陕西汉中城固县高三10月调研数学（理）试卷（解析版） 题型：解答题

    已知椭圆：（）的离心率，且椭圆经过点，直线：与椭圆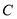交于不同的两点，．

    （1）求椭圆的方程；

    （2）若△的面积为1（为坐标原点），求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源：2017届宁夏高三上月考一数学（文）试卷（解析版） 题型：选择题

    设全集是实数集，，，则图中阴影部分所表示的集合是（ ）

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=$\frac{π}{2}$，平面ABCD⊥平面BCEG，BC=CD=CE=2，AD=BG=1．
    （Ⅰ）求证：DE⊥BC．
    （Ⅱ）求证：AG∥平面BDE；
    （Ⅲ）求几何体EGABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．直线x+$\sqrt{3}$=0的倾斜角为（　　）
    A．60°B．90°C．120°D．不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某市为加强市民的环保意识，组织了“支持环保”签名活动．分别在甲、乙、丙、丁四个不同的场地是进行支持签名获得，统计数据表格如下：
    公园甲乙丙丁
    获得签名人数45603015
    （1）若采用分层抽样的方式从获得签名的人中抽取10名幸运之星，再从10名幸运之星中任选2人接受电视台采访，求这2人来自不同场地的概率；
    （2）电视台记者对场地的签名人进行了是否“支持环保”的问卷调查，统计结果如下（单位：人）；现定义W=|$\frac{a}{a+b}-\frac{c}{c+d}$|，请根据W的值判断，能否在犯错的概率不超过0.01的前提下认为“支持环保”与性别有关．
    有兴趣无兴趣合计
    男25530
    女151530
    合计402060
    临界值表：
    P（K2≥k）0.1000.0500.0100.001
    k2.7063.8416.63510.828
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．其中n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．以下四个命题，其中正确的个数有（　　）
    ①由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，某人数学成绩优秀，则他有99%的可能物理优秀．
    ②两个随机变量相关性越强，则相关系数的绝对值越接近于1；
    ③在线性回归方程$\widehat{y}=0.2x+12$中，当解释变量x每增加一个单位时，预报变量$\widehat{y}$平均增加0.2个单位；
    ④对分类变量X与Y，它们的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握程度越大．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．某四棱锥的三视图如图所示，该四棱锥的体积是（　　）
    A．8$\sqrt{5}$B．$\frac{2\sqrt{5}}{3}$C．$\frac{4\sqrt{5}}{3}$D．$\frac{8\sqrt{5}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知直线l：y=x+b，圆C：x2+y2+2ax-2ay+2a2-4a=0（a＞0）．
    （1）当a=1时，直线l与圆C相切，求b的值；
    （2）当b=1时，是否存在a，使得直线l与圆C相交于A（x1，y1），B（x2，y2）两点，且满足x1x2+y1y2=1？若存在，求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案