
| A. | ①或② | B. | ②或③ | C. | ③或④ | D. | ④或① |
分析 对于①,由正弦定理可得b,利用三角形内角和定理可求C,满足条件的三角形有1个;
对于②,由正弦函数的图象和性质可知当$\frac{1}{2}<sinB<1$时,B有两解,满足条件的三角形有2个;
对于③,由正弦定理可得sinC,结合范围可求C的值有两解,故不正确;
对于④,利用余弦定理即可整理解得唯一确定的c,b,满足条件的三角形有1个.
解答 解:∵A=$\frac{π}{6}$,a=1.
对于:①B=$\frac{π}{4}$,由正弦定理可得:b=$\frac{asinB}{sinA}$=$\sqrt{2}$,C=π-A-B=$\frac{7π}{12}$,满足条件的三角形有1个,故正确;
对于:②b=2sinB,B∈(0,$\frac{5π}{6}$),由正弦函数的图象和性质可知当$\frac{1}{2}<sinB<1$时,即,1<b<2时,B有两解,满足条件的三角形有2个,故不正确;
对于:③c=$\sqrt{3}$,由正弦定理可得:sinC=$\frac{csinA}{a}$=$\frac{\sqrt{3}}{2}$,由C∈(0,$\frac{5π}{6}$),可得:C=$\frac{π}{3}$或$\frac{2π}{3}$,满足条件的三角形有2个,故不正确;
对于:④2c-$\sqrt{3}$b=0,可得:b=$\frac{2c}{\sqrt{3}}$,由余弦定理可得:1=($\frac{2c}{\sqrt{3}}$)2+c2-$\sqrt{3}$×$\frac{2c}{\sqrt{3}}$×c,整理解得:c=$\sqrt{3}$,b=2,满足条件的三角形有1个,故正确;
故选:D.
点评 本题主要考查了正弦定理,三角形内角和定理,两角和的正弦函数公式,正弦函数的图象和性质在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8] | B. | [-8,-4] | C. | (-∞,4]∪[8,+∞) | D. | (-∞,-8]∪[-4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
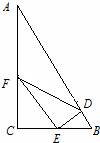 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$1+\frac{{2\sqrt{2}}}{3}$] | B. | $(-∞,\frac{3}{2}+\sqrt{2}]$ | C. | (-∞,6] | D. | (-∞,$3+2\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com