练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

    零件的个数x（个）

    2

    3

    4

    5

    加工的时间y（小时）

    2.5

    3

    4

    4.5

    （1）在给定的坐标系中画出表中数据的散点图；

    （2）求出y关于x的线性回归方程＝bx＋a，

    （3）试预测加工20个零件需要多少小时？

    【答案】（1）详见解析；（2）=0.7x+1.05；（3） 15.05

    【解析】

    试题分析：（1）以表格中的数据作为点的坐标可得到散点图；（2）依据公式将点的坐标代入可求得b,a值，从而确定回归方程；（3）将x=20代入回归方程可得到需要的时间

    试题解析：（1）散点图如下图，

    ；

    （2）由表中数据得：=52.5，，=54，

    ∴b=0.7，∴a=1.05，

    ∴=0.7x+1.05，

    （3）将x=20代入回归直线方程，得=0.7×20+1.05=15.05，

    ∴预测加工20个零件需要15.05小时．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，一直一艘船由岛以海里/小时的速度往北偏东的岛形式，计划到达岛后停留分钟后继续以相同的速度驶往岛.岛在岛的北偏西的方向上，岛也也在岛的北偏西的方向上.上午时整，该船从岛出发.上午时分，该船到达处，此时测得岛在北偏西的方向上.如果一切正常，此船何时能到达岛？（精确到分钟）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知曲线C的参数方程为 （α为参数），以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标轴方程为ρcos（θ﹣ ）=2 ．
    （1）求曲线C的普通方程与直线l的直角坐标方程；
    （2）设点P为曲线C上的动点，求点P到直线l距离的最大值及其对应的点P的直角坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点，焦点在轴上，离心率为的椭圆过点．

    （1）求椭圆的方程；

    （2）设不过原点的直线与该椭圆交于两点，满足直线的斜率依次成等比数列，求面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了了解一年内的用水情况，抽取了10天的用水量如下表所示：

    天数

    1

    1

    1

    2

    2

    1

    2

    用水量／吨

    22

    38

    40

    41

    44

    50

    95

    （Ⅰ）在这10天中，该公司用水量的平均数是多少？每天用水量的中位数是多少？

    （Ⅱ）你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年4月23日“世界读书日”来临之际，某校为了了解中学生课外阅读情况，随机抽取了100名学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.

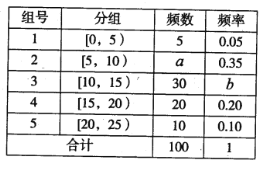
    （Ⅰ）求的值，并作出这些数据的频率分布直方图；

    （Ⅱ）假设每组数据组间是平均分布的，试估计该组数据的平均数；（同一组中的数据用该组区间的中点值作代表）；

    （Ⅲ）现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”，经过比赛后从这6人中选拔2人组成该校代表队，求这2人来自不同组别的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}和{bn}是两个等差数列,记cn=max{b1-a1n,b2-a2n,…,bn-ann}(n=1,2,3,…),其中max{x1,x2,…,xs}表示x1,x2,…,xs这s个数中最大的数.

    (Ⅰ)若an=n,bn=2n-1,求c1,c2,c3的值,并证明{cn}是等差数列;

    (Ⅱ)证明:或者对任意正数M,存在正整数m,当n≥m时, >M;或者存在正整数m,使得cm,cm+1,cm+2,…是等差数列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年4月23日“世界读书日”来临之际，某校为了了解中学生课外阅读情况，随机抽取了100名学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.

    （1）求的值，并作出这些数据的频率分布直方图；

    （2）现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”，经过比赛后从这6人中选拔2人组成该校代表队，求这2人来自不同组别的概率；

    （3）假设每组数据组间是平均分布的，若该校希望使15%的学生的一周课外阅读时间不低于（小时）的时间，作为评选该校“课外阅读能手”的依据，试估计该值，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（选修4﹣4：坐标系与参数方程）
    已知曲线C1的参数方程为 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．
    （1）把C1的参数方程化为极坐标方程；
    （2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）

    查看答案和解析>>

    同步练习册答案