
分析 (1)求得圆心到直线的距离,运用弦长公式,由离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(2)设过P的椭圆E的切线l0的方程为y-y0=k(x-x0),代入椭圆方程,运用直线和椭圆相切的条件:判别式为0,化简整理,再由韦达定理,即可得到斜率之积为定值.
解答 解:(1)设椭圆半焦距为c,
圆心O到l的距离d=$\frac{\sqrt{6}}{\sqrt{1+1}}$=$\sqrt{3}$,
则l被圆O截得的弦长为2$\sqrt{5-3}$=2$\sqrt{2}$,
所以b=$\sqrt{2}$.
由题意得$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,且a2-b2=c2,
∴a2=3,b2=2,
∴椭圆E的方程为$\frac{{y}^{2}}{3}$+$\frac{{x}^{2}}{2}$=1;
(2)过P(x0,y0)的直线与椭圆E分别只有唯一的公共点,
设过P的椭圆E的切线l0的方程为y-y0=k(x-x0),
整理得y=kx+y0-kx0,
联立直线l0与椭圆E的方程得$\left\{\begin{array}{l}{y=kx+{y}_{0}-k{x}_{0}}\\{2{y}^{2}+3{x}^{2}=6}\end{array}\right.$,
消去y得2[kx+(y0-kx0)]2+3x2-6=0,
整理得(3+2k2)x2+4k(y0-kx0)x+2(kx0-y0)2-6=0,
∵l0与与椭圆E分别只有唯一的公共点(即与椭圆E相切),
∴△=[4k(y0-kx0)]2-4(3+2k2)[2(kx0-y0)2-6]=0,
整理得(2-x${\;}_{0}^{2}$)k2+2x0y0k-(y${\;}_{0}^{2}$-3)=0,
设满足题意的与椭圆E分别只有唯一的公共点的直线的斜率分别为k1,k2,
则k1k2=-$\frac{{{y}_{0}}^{2}-3}{2-{{x}_{0}}^{2}}$.
∵点P在圆O上,∴x02+y02=5,
∴k1k2=-$\frac{5-{{x}_{0}}^{2}-3}{2-{{x}_{0}}^{2}}$=-1.
∴两条切线斜率之积为-1.
点评 本题考查椭圆的方程的求法,运用离心率公式和圆的弦长公式,考查直线和椭圆方程联立,运用韦达定理和直线和椭圆相切的条件:判别式为0,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
| 134 | 112 | 117 | 126 | 128 | 124 | 122 | 116 | 113 | 107 |
| 116 | 132 | 127 | 128 | 126 | 121 | 120 | 118 | 108 | 110 |
| 133 | 130 | 124 | 116 | 117 | 123 | 122 | 120 | 112 | 112 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
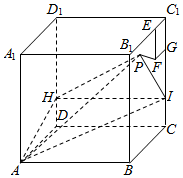 如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )
如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )| A. | $\frac{2\sqrt{17}}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{2\sqrt{17}}{3}$(10-3$\sqrt{2}$) | D. | $\frac{20}{3}$-2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
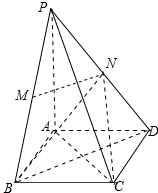 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 12$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{63\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{{45\sqrt{3}}}{4}$ | D. | $\frac{{15\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com