
分析 由已知可得$\sqrt{{a}_{n+1}}=\frac{\sqrt{{a}_{n}}}{\sqrt{{a}_{n}}+1}$,取倒数后可得数列{$\frac{1}{\sqrt{{a}_{n}}}$}是以1为首项,以1为公差的等差数列,然后由等差数列的通项公式得答案.
解答 解:由f(x)=$\frac{x}{x+1}$,且$\sqrt{{a}_{n+1}}$=f($\sqrt{{a}_{n}}$),
得$\sqrt{{a}_{n+1}}=\frac{\sqrt{{a}_{n}}}{\sqrt{{a}_{n}}+1}$,
∴$\frac{1}{\sqrt{{a}_{n+1}}}=\frac{1}{\sqrt{{a}_{n}}}+1$,即$\frac{1}{\sqrt{{a}_{n}+1}}-\frac{1}{\sqrt{{a}_{n}}}=1$,
又a1=1,
∴数列{$\frac{1}{\sqrt{{a}_{n}}}$}是以1为首项,以1为公差的等差数列,
则$\frac{1}{\sqrt{{a}_{n}}}=1+1×(n-1)=n$,
∴${a}_{n}=\frac{1}{{n}^{2}}$.
点评 本题考查数列递推式,考查了数列的函数特性,考查等差关系的确定,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2019<x<0} | B. | {x|x<-2019} | C. | {x|-2019<x<-2015} | D. | {x|-2011<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | ±2 | C. | 2 | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
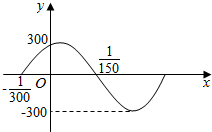 如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )
如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )| A. | y=300sin(50πt+$\frac{π}{3}$) | B. | y=300sin(50πt-$\frac{π}{3}$) | ||
| C. | y=300sin(100πt+$\frac{π}{3}$) | D. | y=300sin(100πt-$\frac{π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com