
在平面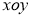 内,不等式
内,不等式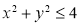 确定的平面区域为
确定的平面区域为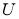 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为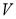 .
.
(1)定义横、纵坐标为整数的点为“整点”.在区域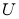 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域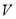 的概率;
的概率;
(2)在区域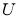 每次任取
每次任取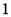 个点,连续取
个点,连续取 次,得到
次,得到 个点,记这
个点,记这 个点在区域
个点在区域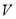 的个数为
的个数为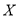 ,求
,求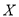 的分布列和数学期望.
的分布列和数学期望.
(1)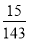
(2)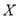 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
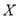 的数学期望为
的数学期望为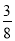 .
.
【解析】
试题分析:(1)作出平面区域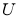 和平面区域
和平面区域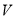 ,打出网格,找出整点,数出在区域
,打出网格,找出整点,数出在区域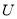 中整点的个数及这些点落在区域
中整点的个数及这些点落在区域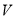 中的个数,运用排列组合知识和古典概型公式求出所求事件的概率;(2)由独立重复试验的概念知,每次在区域
中的个数,运用排列组合知识和古典概型公式求出所求事件的概率;(2)由独立重复试验的概念知,每次在区域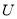 中取一点该点落在区域
中取一点该点落在区域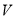 内的概率为定值,取3次,的3个点,落在区域
内的概率为定值,取3次,的3个点,落在区域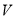 内点的个数服从二项分布,根据二项分布的概率公式和期望公式即可求出分布列与期望.
内点的个数服从二项分布,根据二项分布的概率公式和期望公式即可求出分布列与期望.
试题解析:(1)依题可知平面区域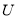 的整点为:
的整点为: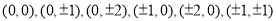 共有13个,上述整点在平面区域
共有13个,上述整点在平面区域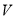 的为:
的为: 共有3个,
共有3个,
∴ . (4分)
. (4分)
(2)依题可得,平面区域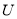 的面积为
的面积为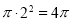 ,
,
平面区域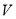 与平面区域
与平面区域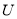 相交部分的面积为
相交部分的面积为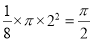 .
.
(设扇形区域中心角为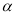 ,则
,则 得
得 ,也可用向量的夹角公式求
,也可用向量的夹角公式求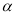 ).
).
在区域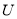 任取1个点,则该点在区域
任取1个点,则该点在区域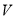 的概率为
的概率为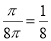 ,随机变量
,随机变量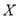 的可能取值为:
的可能取值为: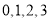 .
.
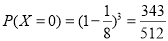 ,
, ,
,
 ,
,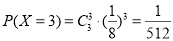 ,
,
∴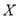 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴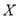 的数学期望:
的数学期望: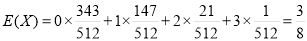 . (12分)
. (12分)
(或者: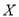 ~
~ ,故
,故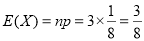 ).
).
考点:二元一次不等式组表示的平面区域,古典概型,二项分布


科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
如图,把周长为1的圆的圆心C放在y轴上,顶点A(0,1),一动点M从A开始逆时针绕圆运动一周,记弧AM=x,直线AM与x轴交于点N(t,0),则函数 的图像大致为( )
的图像大致为( )

查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设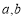 是关于t的方程
是关于t的方程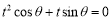 的两个不等实根,则过
的两个不等实根,则过 ,
,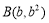 两点的直线与双曲线
两点的直线与双曲线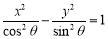 的公共点的个数为( )
的公共点的个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com