
【题目】如图,已知抛物线E:![]() (
(![]() )与圆O:
)与圆O:![]() 相交于A,B两点,且
相交于A,B两点,且![]() .过劣弧
.过劣弧![]() 上的动点
上的动点![]() 作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线
作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线![]() ,
,![]() ,相交于点M.
,相交于点M.
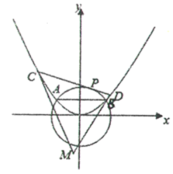
(1)求抛物线E的方程;
(2)求点M到直线![]() 距离的最大值.
距离的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用![]() 求得圆心
求得圆心![]() 到弦
到弦![]() 的距离为1,即可求得点
的距离为1,即可求得点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线方程可得
代入抛物线方程可得![]() ,问题得解
,问题得解
(2)设![]() ,
,![]() ,分别求得
,分别求得![]() 与
与![]() 的方程,即可求得点
的方程,即可求得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,联立直线
,联立直线![]() 的方程和抛物线方程可得:
的方程和抛物线方程可得:![]() ,
,![]() ,即可得点
,即可得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,再由点到直线距离公式可得点M到直线
,再由点到直线距离公式可得点M到直线![]() 的距离为:
的距离为: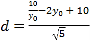 ,
,![]() ,利用其单调性可得:
,利用其单调性可得:![]() ,问题得解
,问题得解
(1)![]()
![]() ,且B在圆上,
,且B在圆上,
所以圆心![]() 到弦
到弦![]() 的距离
的距离![]()
由抛物线和圆的对称性可得![]() ,
,
代入抛物线可得![]() ,解得
,解得![]() ,
,
∴抛物线E的方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ——①,
——①,
同理![]() 的方程为:
的方程为:![]() ——②,
——②,
联立①②解得![]() ,
,![]() ,
,
又直线![]() 与圆
与圆![]() 切于点
切于点![]() ,
,
易得![]() 方程为
方程为![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,
联立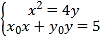 ,化简得
,化简得![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴点M到直线![]() 的距离为:
的距离为:
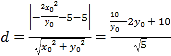 ,
,![]()
易知d关于![]() 单调递减,
单调递减,![]() ,
,
即点M到直线![]() 距离的最大值为
距离的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:![]() 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A.1.2天B.1.8天
C.2.5天D.3.5天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着2022年北京冬奥会的临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放.如图是2012-2018年中国雪场滑雪人数(单位:万人)与同比增长情况统计图则下面结论中正确的是( ).
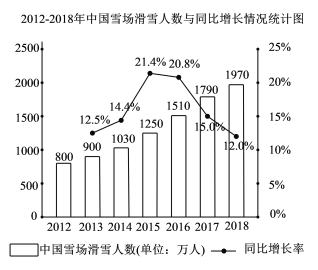
A.2012-2018年,中国雪场滑雪人数逐年增加;
B.2013-2015年,中国雪场滑雪人数和同比增长率均逐年增加;
C.中国雪场2015年比2014年增加的滑雪人数和2018年比2017年增加的滑雪人数均为220万人,因此这两年的同比增长率均有提高;
D.2016-2018年,中国雪场滑雪人数的增长率约为23.4%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 的左、右焦点分别为F1,F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
的左、右焦点分别为F1,F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
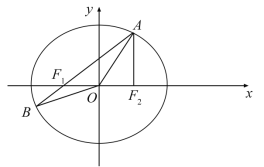
(1)求△AF1F2的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求![]() 的最小值;
的最小值;
(3)设点M在椭圆E上,记△OAB与△MAB的面积分别为S1,S2,若S2=3S1,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
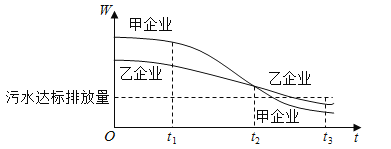
【题目】为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为![]() ,用
,用![]() 的大小评价在
的大小评价在![]() 这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
①在![]() 这段时间内,甲企业的污水治理能力比乙企业强;
这段时间内,甲企业的污水治理能力比乙企业强;
②在![]() 时刻,甲企业的污水治理能力比乙企业强;
时刻,甲企业的污水治理能力比乙企业强;
③在![]() 时刻,甲、乙两企业的污水排放都已达标;
时刻,甲、乙两企业的污水排放都已达标;
④甲企业在![]() 这三段时间中,在
这三段时间中,在![]() 的污水治理能力最强.
的污水治理能力最强.
其中所有正确结论的序号是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com