
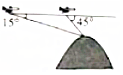
 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )| A. | 2.65千米 | B. | 7.35千米 | C. | 10千米 | D. | 10.5千米 |
分析 利用正弦定理求出飞机到山顶的距离,再利用三角函数的定义得出山顶道飞机航向的距离,从而得出山顶海拔.
解答 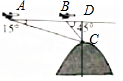 解:设飞机先后飞过的两个位置为A,B,山顶为C,过C作AB的垂线,垂足为D,
解:设飞机先后飞过的两个位置为A,B,山顶为C,过C作AB的垂线,垂足为D,
由题意可知AB=180×$\frac{420}{3600}$=21千米,∠BAC=15°,∠ABC=135°,
∴∠ACB=30°,
在△ABC中,由正弦定理得$\frac{AB}{sin∠ACB}=\frac{AC}{sin∠ABC}$,即$\frac{21}{sin30°}=\frac{AC}{sin135°}$,
∴AC=$\frac{21sin135°}{sin30°}$=21$\sqrt{2}$,
∴CD=ACsin∠BAC=21$\sqrt{2}$•sin15°=$\frac{21(\sqrt{3}-1)}{2}$≈7.35千米,
∴山顶海拔高度h=10-7.35=2.65千米.
故选:A.
点评 本题考查了解三角形的实际应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 合计 | |
| 男同学 | 24 | 6 | 30 |
| 女同学 | 6 | 14 | 20 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
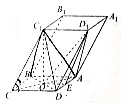 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | ($\frac{4}{3}$,0) | ||
| C. | (-∞,0)∪($\frac{4}{3}$,0) | D. | (-∞,-$\frac{1}{3}$)∪(-$\frac{1}{3}$,0)∪($\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {1,2,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3e-4,1) | B. | [-3e-4,1)∪{-e-2} | C. | [0,1)∪{-e-2} | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com