
| A. | 114 | B. | 96 | C. | 84 | D. | 48 |
分析 四个不同的球全部放入4个不同的盒子内,恰有两个盒子不放球的不同放法的求法,分为两步来求解,先把四个球分为两组,再取两个盒子,作全排列,由于四个球分两组有两种分法,一种是2,2,另一种是3,1,故此题分为两类来求解,再求出它们的和,然后选出正确选项
解答 解:四个球分为两组有两种分法,(2,2),(3,1),
若两组每组有两个球,不同的分法有$\frac{{C}_{4}^{2}}{{A}_{2}^{2}}$=3种,恰有两个盒子不放球的不同放法是3×A42=36种,
若两组一组为3,一组为1个球,不同分法有C43=4种恰有两个盒子不放球的不同放法是4×A42=48种,
综上恰有两个盒子不放球的不同放法是36+48=84种,
故选:C.
点评 本题考查察排列、组合的实际应用,解题的关键是理解事件“四个不同的球全部放入4个不同的盒子内,恰有两个盒子不放球”,宜先将四个球分为两组,再放入,分步求不同的放法种数


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | Sn<2Tn | B. | b4=0 | C. | T7>b7 | D. | T5=T6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $-\frac{{\sqrt{6}-\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
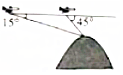 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )| A. | 2.65千米 | B. | 7.35千米 | C. | 10千米 | D. | 10.5千米 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com