
分析 设$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为θ,则$\overrightarrow{b}$与$\overrightarrow{c}$的夹角为$\frac{π}{2}$+θ,设|$\overrightarrow{c}$|=x,根据题意可得x=$\frac{\sqrt{5}}{2}$cos(θ+φ),利用三角函数的性质即可求出最大值
解答 解:∵向量$\overrightarrow a$,$\overrightarrow{b}$为两个互相垂直的单位向量,
设$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为θ,则$\overrightarrow{b}$与$\overrightarrow{c}$的夹角为$\frac{π}{2}$+θ,设|$\overrightarrow{c}$|=x,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$•$\overrightarrow{c}$=|$\overrightarrow{a}$|•|$\overrightarrow{c}$|=xcosθ,$\overrightarrow{b}$•$\overrightarrow{c}$=|$\overrightarrow{b}$|•|$\overrightarrow{c}$|=xcos(θ+$\frac{π}{2}$)=-xsinθ,
∵$(\overrightarrow a-\overrightarrow c)•(\overrightarrow b-2\overrightarrow c)$=0
∴$\overrightarrow{a}$•$\overrightarrow{b}$-2$\overrightarrow{a}$$•\overrightarrow{c}$-$\overrightarrow{b}$•$\overrightarrow{c}$+2${\overrightarrow{c}}^{2}$=2x2-2xcosθ+xsinθ=0,
∴x=cosθ-$\frac{1}{2}$sinθ=$\frac{\sqrt{5}}{2}$cos(θ+φ),其中cosφ=$\frac{2\sqrt{5}}{5}$,sinφ=$\frac{\sqrt{5}}{5}$,
∴0≤x≤$\frac{\sqrt{5}}{2}$,
若设$\overrightarrow{b}$与$\overrightarrow{c}$的夹角为$\frac{π}{2}$-θ,
同理可得0≤x≤$\frac{\sqrt{5}}{2}$,
故$|\overrightarrow c{|_{max}}$=$\frac{{\sqrt{5}}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查了向量的数量积公式和三角函数的图象和性质,属于中档题


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
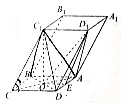 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {1,2,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
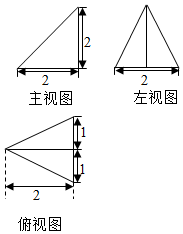 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3e-4,1) | B. | [-3e-4,1)∪{-e-2} | C. | [0,1)∪{-e-2} | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com