
| A. | Sn<2Tn | B. | b4=0 | C. | T7>b7 | D. | T5=T6 |
分析 先求出${S}_{n}={n}^{2}-10n$,从而an=2n-11.由等差数列{bn}满足bn+bn+1=an(n∈N*),求出{bn}是公差d=1,首项b1=-5的等差数列,由此能求出结果.
解答 解:∵数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在函数y=x2-10x的图象上,
∴${S}_{n}={n}^{2}-10n$,
∴a1=1-10=-9,
an=Sn-Sn-1=(n2-10n)-[(n-1)2-10(n-1)]=2n-11,(n≥2)
当n=1时,an=2-11=-9=a1,
∴an=2n-11.
∵等差数列{bn}满足bn+bn+1=an(n∈N*),
∴b1+b2=-9,b2+b3=a2=4-11=-7,
(b2+b3)-(b1+b2)=b3-b1=2d=-7+9=2,
∴d=1,b1=-5,
∴Tn=-5n+$\frac{n(n-1)}{2}×1$=$\frac{{n}^{2}-11n}{2}$.
在A 中,Sn-2Tn=(n2-10n)-(n2-11n)=n>0,∴Sn>2Tn,故A错误;
在B中,b4=-5+3×1=-2,故B错误;
在C中,T7-b7=[7×(-5)+$\frac{7×6}{2}×1$]-(-5+6)=-14-1=-15<0,
∴T7<b7,故C错误;
在D中,T5-T6=[5×(-5)+$\frac{5×4}{2}×1$]-[6×(-5)-$\frac{6×5}{2}×1$]=0,
∴T5=T6,故D正确.
故选:D.
点评 本题考查命题真假的判断,涉及到函数性质、等差数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
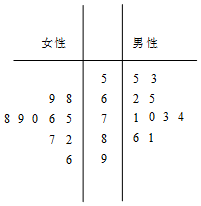 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com