
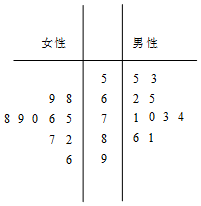
 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:分析 (1)根据茎叶图中的数据,利用平均数和中位数的公式进行计算即可.
(2)根据古典概型的概率公式分别进行计算即可.
解答 解:(1)男性的平均数为$\frac{1}{10}$(55+53+62+65+71+70+73+74+86+81)=$\frac{690}{10}$=69,
女性的中位数为$\frac{76+78}{2}$=77
(2)打分在70分以下(不含70分)的市民中有6名,女性2名,男性4名,
从中抽取3人有${C}_{6}^{3}$=20种方法,有女性被抽中有${C}_{2}^{1}{C}_{4}^{2}+{C}_{2}^{2}{C}_{4}^{1}$=12+4=16,
则对应的概率P=$\frac{16}{20}$=$\frac{4}{5}$.
点评 本题主要考查茎叶图中的应用,结合平均数,中位数的定义和公式以及古典概型的概率公式是解决本题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3\sqrt{7}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn<2Tn | B. | b4=0 | C. | T7>b7 | D. | T5=T6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com