
| A. | $\frac{1}{10}$ | B. | $\frac{2}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{15}$ |
分析 根据题意,分析可得在“波浪数”中,十位数字,千位数字中必有一个是5、另一数是3或4;据此分2种情况讨论,分别求出每种情况下的“波浪数”的个数,由分类计数原理计算可得答案.
解答 解:根据题意,分析可得在“波浪数”中,十位数字,千位数字中必有一个是5、另一数是3或4;
另一数是4时,将5与4放在千位、十位上,有A22种情况,剩余的1、2、3放在其余三个数位上,有A33种情况,
则此时的“波浪数”有A22A33=12个;
另一数3时,4、5必须相邻,有45132;45231;13254;23154四个“波浪数”.
则由1,2,3,4,5可构成数字不重复的五位“波浪数”个数为12+4=16;
可得:这个数为“波浪数”的概率是$\frac{16}{5×4×3×2×1}$=$\frac{2}{15}$.
故选:B.
点评 本题考查排列组合及简单计数问题,解题的关键是理解“波浪数”的含义,进而转化为排列、组合问题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
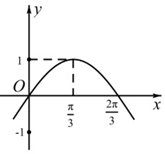 已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
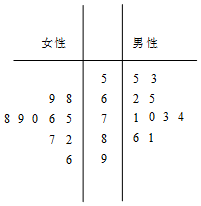 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)可能没有零点 | B. | g(x)可能有1个零点 | C. | g(x)可能有2个零点 | D. | g(x)可能有3个零点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com