
分析 由y=tanx的单调递增区间为(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)(k∈Z),要求$y=2tan({2x+\frac{π}{4}})$的单调递增区间,由2x+$\frac{π}{4}$∈(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)即可求其的单调递增区间.
解答 解:∵y=tanx的单调递增区间为(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)(k∈Z),
令kπ-$\frac{π}{2}$<2x+$\frac{π}{4}$<kπ+$\frac{π}{2}$,解得$\frac{kπ}{2}$-$\frac{3π}{8}$<x<$\frac{kπ}{2}$+$\frac{π}{8}$,(k∈Z),
函数y=2tan(2x+$\frac{π}{4}$)的单调递增区间是:($\frac{kπ}{2}$-$\frac{3π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$),(k∈Z).
故答案为:($\frac{kπ}{2}$-$\frac{3π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$),(k∈Z)
点评 本题考查正切函数的单调性,着重考查学生整体代换的数学思想,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
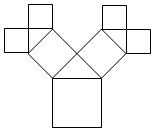 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com