
 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点.分析 (1)连接BD,证明:BN⊥CD,PD⊥BN,即可证明BN⊥平面PCD;
(2)假设线段PC上存在一点H,连接MH,DH,MD,可得∠MHD为MH与平面PCD所成的角,在直角三角形MDH中,$DM=\sqrt{3}$,当DH最小,即DH⊥PC时,∠DHM最大,利用条件求出CH,即可得出结论.
解答 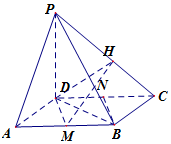 (1)证明:连接BD,
(1)证明:连接BD,
∵四边形ABCD为菱形,∠BCD=∠BAD=60°
∴△BCD为正三角形,∵N为CD中点,所以BN⊥CD…(2分)
∵PD⊥平面ABCD,BN?平面ABCD,∴PD⊥BN,….(4分)
又PD?平面PCD,CD?平面PCD,CD∩PD=D,∴BN⊥平面PCD…6 分
(2)解:假设线段PC上存在一点H,连接MH,DH,MD,
MBDN为平行四边形,∴MD∥BN,
由(1)BN⊥平面PCD∴MD⊥平面PCD,∴∠MHD为MH与平面PCD所成的角…(9分)
在直角三角形MDH中,$DM=\sqrt{3}$,当DH最小,即DH⊥PC时,∠DHM最大,
$tan∠DHM=\frac{DM}{DH}=\frac{{\sqrt{3}}}{DH}=\frac{{\sqrt{6}}}{2}$,
∴$DH=\sqrt{2}$
在Rt△DHC中$DH=\sqrt{2},CD=2$,∴$CH=\sqrt{2}$…(11分)
∴线段PC上存在点H,当$CH=\sqrt{2}$时,使MH与平面PCD所成最大角的正切值为$\frac{{\sqrt{6}}}{2}$…(12分)
点评 本题考查线面垂直的判定,考查线面角,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].
已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $3\sqrt{3}π$ | C. | $\frac{{8\sqrt{2}}}{3}π$ | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
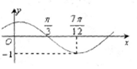 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com