
【题目】已知关于x的函数![]() 与
与![]() 在区间D上恒有
在区间D上恒有![]() .
.
(1)若![]() ,求h(x)的表达式;
,求h(x)的表达式;
(2)若![]() ,求k的取值范围;
,求k的取值范围;
(3)若![]()
![]() 求证:
求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明详见解析
;(3)证明详见解析
【解析】
(1)求得![]() 与
与![]() 的公共点,并求得过该点的公切线方程,由此求得
的公共点,并求得过该点的公切线方程,由此求得![]() 的表达式.
的表达式.
(2)先由![]() ,求得
,求得![]() 的一个取值范围,再由
的一个取值范围,再由![]() ,求得
,求得![]() 的另一个取值范围,从而求得
的另一个取值范围,从而求得![]() 的取值范围.
的取值范围.
(3)先由![]() ,求得
,求得![]() 的取值范围,由方程
的取值范围,由方程![]() 的两个根,求得
的两个根,求得![]() 的表达式,利用导数证得不等式成立.
的表达式,利用导数证得不等式成立.
(1)由题设有![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,所以
,所以![]() .
.
因此![]() 即
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() ,因此
,因此![]() .
.
故![]() .
.
(2)令![]() ,
,![]() .
.
又![]() .
.
若![]() ,则
,则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,则
上递减,则![]() ,即
,即![]() ,不符合题意.
,不符合题意.
当![]() 时,
时,![]() ,符合题意.
,符合题意.
当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,则
上递增,则![]() ,
,
即![]() ,符合题意.
,符合题意.
综上所述,![]() .
.
由![]()
![]()
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 为增函数,
为增函数,
因为![]() ,
,
故存在![]() ,使
,使![]() ,不符合题意.
,不符合题意.
当![]() ,即
,即![]() 时,
时,![]() ,符合题意.
,符合题意.
当![]() ,即
,即![]() 时,则需
时,则需![]() ,解得
,解得![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
(3)因为![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() 对任意
对任意![]() 恒成立,
恒成立,
等价于![]() 对任意
对任意![]() 恒成立.
恒成立.
故![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,
,
当![]() ,
,![]() ,
,
此时![]() ,
,
当![]() ,
,![]() ,
,
但![]() 对任意的
对任意的![]() 恒成立.
恒成立.
等价于![]() 对任意的
对任意的![]() 恒成立.
恒成立.
![]() 的两根为
的两根为![]() ,
,
则![]() ,
,
所以![]()
![]() .
.
令![]() ,则
,则![]() .
.
构造函数![]() ,
,![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 递减,
递减,![]() .
.
所以![]() ,即
,即![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
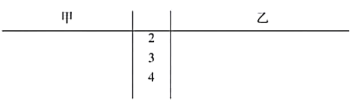
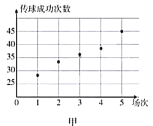
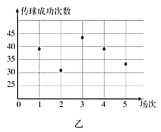
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,右焦点为
,右焦点为![]() ,且
,且![]() ,其中
,其中![]() 为原点.
为原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点![]() 满足
满足![]() ,点
,点![]() 在椭圆上(
在椭圆上(![]() 异于椭圆的顶点),直线
异于椭圆的顶点),直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.求直线
的中点.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点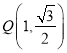 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过原点![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间用一台包装机包装葡萄糖,每袋葡萄糖的重量是一个随机变量,它服从正态分布.当机器工作正常时,每袋葡萄糖平均重量![]() 为0.5kg,标准差
为0.5kg,标准差![]() 为0.015kg.
为0.015kg.
(1)已知包装每袋葡萄糖的成本为1元,若发现包装好的葡萄糖重量异常,则需要将该袋葡萄糖进行重新包装,假设重新包装后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 满足
满足![]() ,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
(2)某日开工后, 为检査该包装机工作是否正常, 随机地抽取它所包装的葡萄糖9袋,若抽取的9袋葡萄糖称得净重(kg)为:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,以
,以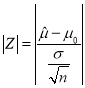 作为检验统计量,其中
作为检验统计量,其中![]() 为样本总数,
为样本总数,![]() 服从正态分布
服从正态分布![]() ,且
,且![]() .
.
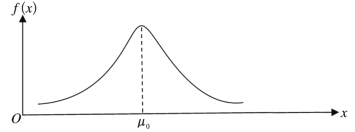
①若机器工作正常时, 每袋葡萄糖的重量服从的正态分布曲线如下图所示,且经计算得上述样本数据的标准差![]() 0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
②若![]() ,就推断该包装机工作异常,这种推断犯错误的概率不超过
,就推断该包装机工作异常,这种推断犯错误的概率不超过![]() ,试以95%的可靠性估计该包装机工作是否正常.
,试以95%的可靠性估计该包装机工作是否正常.
附: 若随机变量![]() 服从正态分布:
服从正态分布:![]() ,
,![]()
![]()
参考数据:![]() ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com