
分析 利用伸缩变换$\left\{\begin{array}{l}x′=\frac{1}{2}x\\ y′=\frac{1}{3}y\end{array}$,可得x=3x′,y=2y′,代入$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,即可得出结论.
解答 解:∵$\left\{\begin{array}{l}x′=\frac{1}{2}x\\ y′=\frac{1}{3}y\end{array}$,
∴x=2x′,y=3y′,
∵$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,
∴x′2-y′2=1,
∴x2-y2=1,
故答案为x2-y2=1.
点评 本题考查伸缩变换,考查双曲线的方程,比较基础.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
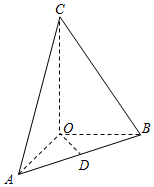 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±1 | C. | 1或2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
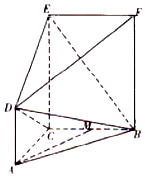 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com