练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．设相交两圆的交点为M和K，引两圆的公切线，切点分别是A、B，证明：∠AMB+∠AKB=180°．

    分析 连接MK并延长交AB于C点，则△ACM∽△ACK，可得∠MAC=∠AKC，同理∠MBC=∠BKC，利用三角形的内角和定理，即可证明结论．

    解答 证明：连接MK并延长交AB于C点，
    则△ACM∽△ACK，∴∠MAC=∠AKC，
    同理∠MBC=∠BKC，
    ∵∠MAB+∠ABM+∠AMB=180°，
    ∴∠AKC+∠BKC+∠AMB=180°，
    ∵∠AKC+∠BKC=∠AKB，
    ∴∠AMB+∠AKB=180°．

    点评 本题考查三角形相似的判定与性质，考查三角形的内角和定理，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线均与圆C：x2+y2-6y+5=0相切，且双曲线的焦距为6，则该双曲线的方程为（　　）
    A．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1B．$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1C．$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1D．$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．按右图所示的程序框图运算，若输入 x=200，则输出 k  的值是（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．P是双曲线$\frac{x^2}{16}-\frac{y^2}{20}=1$上一点，F1，F2分别是双曲线左右焦点，若|PF1|=9，则|PF2|=（　　）
    A．1B．17C．1或17D．以上答案均不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

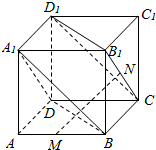    3．如图，正方体ABCD-A1B1C1D1中，M、N分别为AB、B1C的中点．
    （1）用向量法证明平面A1BD∥平面B1CD1；
    （2）用向量法证明MN⊥面A1BD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

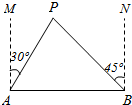    13．如图，A、B两座城市相距100千米，现计划在这两座城市之间修筑一条高等级公路（即线段AB）．经测量，森林保护区中心P点在A城市的北偏东30°方向，B城市的北偏西45°方向上，已知森林保护区的范围在以P为圆心，50千米为半径的圆形区域内．请问：计划修筑的这条高等级公路会不会穿越保护区，为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．行如图所示的程序框图，若输入a=390，b=156，则输出a=（　　）
    A．26B．39C．78D．156

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．韩国首尔医院近20天每天因患中东呼吸综合征而入院就诊的人数依次构成数列{an}，己知a1=1，a2=2，且满足an+2-an=2+2（-1）n，n∈N+，则该医院20天内因患中东呼吸综合征就诊的人数共有210．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．将函数f（x）=$\sqrt{3}$cosx+sinx（x∈R）的图象向右平移m（m＞0）个单位长度后，得到函数g（x）=$\sqrt{3}$sinx+cosx（x∈R）的图象，则m的最小值是$\frac{π}{6}$．

    查看答案和解析>>

    同步练习册答案