练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．求函数$y=\sqrt{{x^2}-8x+17}+\sqrt{{x^2}+4}$的最小值为5．

    分析 根据其几何意义即可求出答案．

    解答 解：函数$y=\sqrt{{x^2}-8x+17}+\sqrt{{x^2}+4}$=$\sqrt{（x-4）^{2}+1}$+$\sqrt{{x}^{2}+4}$=$\sqrt{（x-4）^{2}+（0-1）^{2}}$+$\sqrt{（x-0）^{2}+（0-2）^{2}}$表示x轴上动点P（x，0）到A（4，1）和B（0，-2）的距离和，当
    P为AB与x轴的交点时，函数取最小值|AB|=$\sqrt{（4-0）^{2}+（1+2）^{2}}$=5，
    故答案为：5

    点评 本题考查的知识点是函数的最值及其几何意义，分析出函数表示的几何意义是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．已知a，b＞0，a+2b=1，则t=$\frac{1}{a}$+$\frac{1}{b}$的最小值是（　　）
    A．3+2$\sqrt{2}$B．3-2$\sqrt{2}$C．1+2$\sqrt{2}$D．1+$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在△ABC中，角A．B．C的对边分别为a，b，c，已知A=60°，a=2$\sqrt{3}$，b=2$\sqrt{2}$，则角B=（　　）
    A．45°B．30°C．90°D．45°或135°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=cos（2x-\frac{π}{3}）+2sin（x-\frac{π}{4}）sin（x+\frac{π}{4}）$．
    （1）求函数f（x）的单调递增区间；
    （2）将y=f（x）的图象向左平移$\frac{π}{3}$个单位长度，再将得到的图象横坐标变为原来的2倍（纵坐标不变），得到y=g（x）的图象；若函数y=g（x）在区间$（\frac{π}{2}，\frac{13π}{4}）$上的图象与直线y=a有三个交点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．最近，国家统计局公布：2015年我国经济增速为6.9%，创近25年新低．在当前经济增速放缓的情况下，转变经济发展方式，淘汰落后产能，寻找新的经济增长点是当务之急．为此，经济改革专家组到基层调研，由一幅反映某厂6年来这种产品的总产量C与时间t（年）的函数关系图初步了解到：某工厂6年来生产某种产品的情况是：前3年年产量的增长速度越来越快，后3年年产量保持不变，则他们看到的图是（　　）
    A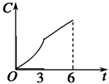．B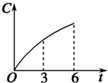．C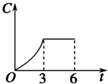．D．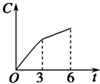

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow a=（2，1），\overrightarrow b=（3，m）$，若向量$（2\overrightarrow a-\overrightarrow b）$与向量$\overrightarrow b$共线，则$|{\overrightarrow b}|$=（　　）
    A．$\frac{{3\sqrt{5}}}{2}$B．$3\sqrt{5}$C．$\frac{{3\sqrt{7}}}{2}$D．$3\sqrt{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若三个实数2，m，6成等差数列，则m的值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某品牌汽车的4S店对最近60位采用分期付款的购车者人数进行统计，统计结果如下表所示：
    付款方式分1期分2期分3期分4期
    频数20a14b
    已知分4期付款的频率为$\frac{1}{6}$，并且4S店销售一辆该品牌的汽车，顾客分1期付款其利润为1万元，分2期或3期付款其利润为2万元，分4期付款其利润为3万元，以频率作为概率．
    （1）求事件A“购买该品牌汽车的3位顾客中，至多有1位分4期付款”的概率；
    （2）用X表示销售一两该品牌汽车的利润，求X的分布列及数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知F是抛物线C：y2=2px（p＞0）的焦点，点P（1，t）在抛物线C上，且|PF|=$\frac{3}{2}$．
    （1）求p，t的值；
    （2）设O为坐标原点，抛物线C 上是否存在点A（A与O不重合），使得过点O作线段OA的垂线与抛物线C交于点B，直线AB分别交x轴、y轴于点D，E，且满足S△OAB=$\frac{3}{2}{S_{△ODE}}$（S△OAB表示△OAB的面积，S△ODE表示△ODE的面积）？若存在，求出点A的坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案