
���� ��1�������������ϵĵ㵽������ߵľ�����ȣ��ɵ�pֵ�������ɵ�tֵ��
��2�������⣬ֱ��OA��б�ʴ��ڣ��Ҳ�Ϊ0�����������ߵĶԳ��ԣ�����A�ڵ�һ���ޣ����ֱ�߷����������߷����������ɵ�A��B�����꣬�����ɵ�E�����꣬����S��OAB=$\frac{3}{2}{S_{��ODE}}$�����ɵó����ۣ�
��� �⣺�ߵ� P��1��t��Ϊ������y2=2px��p��0����һ�㣬F�������ߵĽ��㣬|PF|=$\frac{3}{2}$��
��1+$\frac{p}{2}$=$\frac{3}{2}$��
��ã�p=1��
�������ߵķ���Ϊ��y2=2x��
��x=1����ɵã�t=��$\sqrt{2}$��
��2�������⣬ֱ��OA��б�ʴ��ڣ��Ҳ�Ϊ0�����������ߵĶԳ��ԣ�����A�ڵ�һ���ޣ�
��ֱ��OA�ķ���Ϊy=kx��k��0����OA��OB��ֱ��OB�ķ���Ϊy=-$\frac{1}{k}$x��
��$\left\{\begin{array}{l}{{y}^{2}=2x}\\{y=kx}\end{array}\right.$����k2x2=2x����x=0����ȥ����x=$\frac{2}{{k}^{2}}$����A��$\frac{2}{{k}^{2}}$��$\frac{2}{k}$����
ͬ��B��2k2��-2k����
��k=1ʱ��AB��y�ᣬ���������⣬
��ֱ��AB�ķ���Ϊy+2k=$\frac{\frac{2}{k}+2k}{\frac{2}{{k}^{2}+2{k}^{2}}}$��x-2k2����
��y+2k=$\frac{k}{1-{k}^{2}}$��x-2k2����
��E��0��$\frac{-2k}{1-{k}^{2}}$����
��S��OAB=$\frac{3}{2}{S_{��ODE}}$��
��|yA|+|yB|=$\frac{3}{2}$|yE|��
��yA��yB��ţ�
��|yA|+|yB|=|yA-yB|=$\frac{3}{2}$|yE|��
��|$\frac{2}{k}+2k$|=$\frac{3}{2}$•|$\frac{-2k}{1-{k}^{2}}$|
��k2=$\frac{1}{2}$��2��
��A��4��2$\sqrt{2}$����A��1��$\sqrt{2}$����
�ɶԳ��ԣ��ɵ�A��4����2$\sqrt{2}$����A��1����$\sqrt{2}$����
���� ���⿼�������ߵķ��������ʣ�����ֱ���������ߵ�λ�ù�ϵ������ѧ�������������������������е��⣮


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
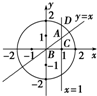 ֱ��x=1��y=x����Բx2+y2=4�ֳ�A��B��C��D�ĸ�������ͼ�����ֲ�ͬ����ɫ������Ϳɫ��Ҫ�ߵ���������ɫ���죬ÿ������ֻͿһ����ɫ�����ж����ֲ�ͬ��Ϳɫ������
ֱ��x=1��y=x����Բx2+y2=4�ֳ�A��B��C��D�ĸ�������ͼ�����ֲ�ͬ����ɫ������Ϳɫ��Ҫ�ߵ���������ɫ���죬ÿ������ֻͿһ����ɫ�����ж����ֲ�ͬ��Ϳɫ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com