
分析 (Ⅰ)利用性质对任意的x,y∈A,x,y∈A(x≠y),都有$|{x-y}|>\frac{xy}{25}$,代入可判断
(Ⅱ)依题意有:${|a}_{i}-{a}_{i+1}|≥\frac{{a}_{i}{a}_{i+1}}{25}$(i=1,2,3…n-1),又a1<a2<…<an,因此:${a}_{i+1}-{a}_{i}≥\frac{{a}_{i}{a}_{i+1}}{25}$(i=1,2,3…n-1),由此能够证明:$\frac{1}{a_1}-\frac{1}{a_n}≥\frac{n-1}{25}$.
(Ⅲ)由$\frac{1}{a_1}≥\frac{n-1}{25}$,a≥1可得由$1>\frac{n-1}{25}$,因此n<26,同理$\frac{1}{{a}_{i}}-\frac{1}{{a}_{n}}≥\frac{n-i}{25}$,可得,$\frac{1}{{a}_{i}}>\frac{n-i}{25}$.由此能够推导出集合A中元素个数的最大值.
解答 解:(I)由于|1-2|≥$\frac{1×2}{25}$,|1-3|≥$\frac{1×3}{25}$,|1-4|$≥\frac{1×4}{25}$,|2-3|≥$\frac{2×3}{25}$,|2-4|$≥\frac{2×4}{25}$,|3-4|$≥\frac{3×4}{25}$
∴集合{1,2,3,4}具有性质P;
(Ⅱ)依题意有:${|a}_{i}-{a}_{i+1}|≥\frac{{a}_{i}{a}_{i+1}}{25}$(i=1,2,3…n-1),又a1<a2<…<an,
因此:${a}_{i+1}-{a}_{i}≥\frac{{a}_{i}{a}_{i+1}}{25}$(i=1,2,3…n-1)
可得:$\frac{1}{{a}_{i}}-\frac{1}{{a}_{n+i}}≥\frac{1}{25}$,(i=1,2,3…n-1)
所以有:$\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n}}≥$$\frac{n-1}{25}$,即$\frac{1}{a_1}-\frac{1}{a_n}≥\frac{n-1}{25}$.
得证;
(Ⅲ)由$\frac{1}{a_1}≥\frac{n-1}{25}$,a≥1,可得$1>\frac{n-1}{25}$,因此n<26,同理$\frac{1}{{a}_{i}}-\frac{1}{{a}_{n}}≥\frac{n-i}{25}$,可得,$\frac{1}{{a}_{i}}>\frac{n-i}{25}$.
又∵ai≥i,可得$\frac{1}{i}>\frac{n-i}{25}$,那么:25>i(n-i),(i=1,2,3…n-1)也均成立.
当n≥10时,取i=5,则i(n-i)=5(n-5)≥25,可知n<10.
又当n≤9时,$i(n-i)≤(\frac{i+n-i}{2})^{2}=\frac{{n}^{2}}{2}<25$,所以n≤9
因此集合A中元素个数的最大值为9.
点评 本题考查数列的性质的综合运用,解题时要认真审题,注意公式的合理运用,合理地进行等价转化和变形.属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 90° | D. | 45°或135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 |
| 频数 | 20 | a | 14 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
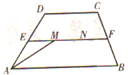 如图,已知四边形ABCD是等腰梯形,E、F是腰AD、BC中点,M、N是EF两个三等分点,下底是上底2倍,若向量$\overrightarrow{AB}$=$\overrightarrow{a}$,向量$\overrightarrow{BC}$=$\overrightarrow{b}$,则向量$\overrightarrow{AM}$用$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,已知四边形ABCD是等腰梯形,E、F是腰AD、BC中点,M、N是EF两个三等分点,下底是上底2倍,若向量$\overrightarrow{AB}$=$\overrightarrow{a}$,向量$\overrightarrow{BC}$=$\overrightarrow{b}$,则向量$\overrightarrow{AM}$用$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\frac{1}{2}$($\overrightarrow{a}+\overrightarrow{b}$) | B. | -$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$ | D. | $\frac{1}{3}\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com