
分析 曲线C为ρ=4cosθ+2sinθ,即ρ2=4ρcosθ+2ρsinθ,利用互化公式可得直角坐标方程:(x-2)2+(y-1)2=5.令x=2+$\sqrt{5}$cosα,y=1+$\sqrt{5}$sinα.化简即可得出.
解答 解:曲线C为ρ=4cosθ+2sinθ,即ρ2=4ρcosθ+2ρsinθ,可得直角坐标方程:x2+y2=4x+2y,配方为:(x-2)2+(y-1)2=5.
令x=2+$\sqrt{5}$cosα,y=1+$\sqrt{5}$sinα.
则x-y=2+$\sqrt{5}$cosα-(1+$\sqrt{5}$sinα)=1+$\sqrt{5}$(cosα-sinα)=1+$\sqrt{10}$$sin(\frac{π}{4}-α)$∈$[1-\sqrt{10},1+\sqrt{10}]$.
∴x-y的取值范围为$[1-\sqrt{10},1+\sqrt{10}]$.
点评 本题考查了圆的极坐标方程、圆的参数方程、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
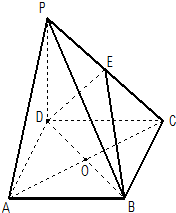 如图,在四棱锥P-ABCD中,底面ABCD是棱长为a正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,AC与BD交于O点.
如图,在四棱锥P-ABCD中,底面ABCD是棱长为a正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,AC与BD交于O点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
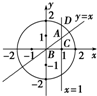 直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?
直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com