
分析 (1)由等差数列等差中项的性质可知:2(a3+a5)=a4+a6,即可求得公比q,由等比数列前n项和公式,即可求得Sn,根据等差{bn}的前三项为b1=2,b2=5,b3=8,即b1=2,d=3,即可求得数列{bn}的通项公式;
(2)由$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{(3n-1)(3n+2)}=\frac{1}{3}(\frac{1}{3n-1}-\frac{1}{3n+2})$,利用“裂项法”即可求得Tn,?n∈Z,$\frac{1}{10}≤{T_n}<\frac{1}{6}$,由Tnbm≤1知只要存在正整数m使${b_m}≤\frac{1}{T_n}$,代入即可求得正整数m的最大值.
解答 解:(1)设等比数列{an}的公比为q,由a3=1且a4,a3+a5,a6为等差数列{bn}(n∈N*)三项,
则2(a3+a5)=a4+a6,得2(1+q2)=q+q3=q(1+q2),得q=2.
从而${S_n}=\frac{1}{4}+\frac{1}{2}+…+{2^{n-3}}=\frac{{\frac{1}{4}(1-{2^n})}}{1-2}={2^{n-2}}-\frac{1}{4}$,
∴{bn}的前三项为b1=2,b2=5,b3=8,
∴公差d=3,
故等差数列的通项公式为bn=3n-1.
(2)由(1)知,$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{(3n-1)(3n+2)}=\frac{1}{3}(\frac{1}{3n-1}-\frac{1}{3n+2})$,
∴数列$\{\frac{1}{{{b_n}{b_{n+1}}}}\}$的前n项和:
${T_n}=\frac{1}{3}[(\frac{1}{2}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{8})+…+(\frac{1}{3n-1}-\frac{1}{3n+2})]$,
=$\frac{1}{3}(\frac{1}{2}-\frac{1}{3n+2})$.
从而得对于?n∈Z,$\frac{1}{10}≤{T_n}<\frac{1}{6}$,故由Tnbm≤1知只要存在正整数m使${b_m}≤\frac{1}{T_n}$,
即只要3m-1≤6,解得$m≤\frac{7}{3}$.
∵m为正整数,
∴m的最大值为2.
点评 本题考查等比数列和等差数列通项公式和前n项和公式的应用,考查“裂项法”求数列的前n项和,不等式恒成立问题的应用,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
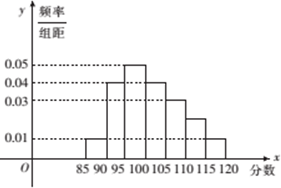 某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.
某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 90° | D. | 45°或135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 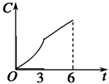 | B. | 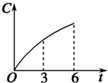 | C. | 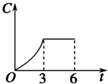 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com