
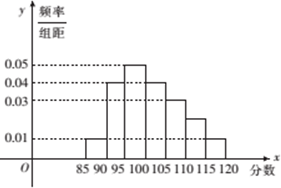
 某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.
某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
分析 (1)求出该班总人数、分数在110-115内的学生的频率,即可得出分数在110-115内的人数;
(2)利用列举法确定基本事件的个数,即可求出其中恰好含有一名女生的概率;
(3)分别求出回归学生的值,代入从而求出线性回归方程,将x=130代入,从而求出y的值.
解答 解:(1)分数在100-110内的学生的频率为P1=(0.04+0.03)×5=0.35,所以该班总人数为$N=\frac{21}{0.35}=60$,
分数在110-115内的学生的频率为P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1,分数在110-115内的人数n=60×0.1=6.
(2)由题意分数在110-115内有6名学生,其中女生有2名,
设男生为A1,A2,A3,A4,女生为B1,B2,
从6名学生中选出3人的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)共15个.
其中恰 好含有一名女生的基本事件为
(A1,B1),(A1,B2),(A2,B2),(A2,B1),(A3,B1),
(A3,B2),(A4,B1),(A4,B2),共8个,
所以所求的概率为$P=\frac{8}{15}$.
(3)$\overline x=100+\frac{-12-17+17-8+8+12}{7}=100$;
$\overline y=100+\frac{-6-9+8-4+4+1+6}{7}=100$;
由于x与y之间具有线性相关关系,
根据回归系数公式得到$\stackrel{∧}{b}$=0.5,$\stackrel{∧}{a}$=100-0.5×100=50,
∴线性回归方程为$\stackrel{∧}{y}$=0.5x+50,
∴当x=130时,$\stackrel{∧}{y}$=115.
点评 本题考查概率的计算,考查物理成绩y与数学成绩x的线性回归方程,考查学生的计算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
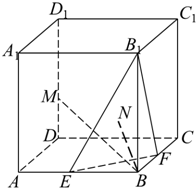 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1} | C. | $\{-1,\frac{{\sqrt{2}}}{2}\}$ | D. | $\{\frac{{\sqrt{2}}}{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 12 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com