
分析 先求得偶函数f(x)的周期为4,根据当x∈[0,2]时,f(x)=2-x2,再画出y=f(x)以及y=2sinx在[-3π,3π]内的图象,数形结合可得结论.
解答 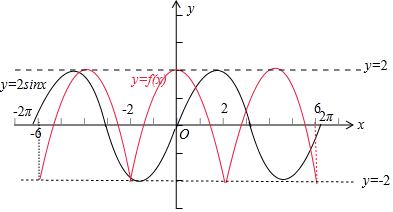 解:定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,即足f(x+2)=-f(x),
解:定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,即足f(x+2)=-f(x),
∴f(x+4)=f(x),故f(x)的周期为4.
且当x∈[0,2]时,f(x)=2-x2,则当x∈[-2,2]时,f(x)=2-x2 .
再画出y=f(x)以及y=2sinx在[-3π,3π]内的图象,如图所示:
数形结合可得函数y=f(x)的图象和函数y=2sinx在[-3π,3π]内的图象的交点个数为5个,
则方程f(x)=2sinx在[-3π,3π]内根的个数是5,
故答案为:5.
点评 本题主要考查函数的奇偶性以及函数的周期性,方程的根的存在性以及个数判断,函数的图象,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3π}{8}+2kπ,\frac{7π}{8}+2kπ}](k∈Z)$ | B. | $[{-\frac{π}{8}+2kπ,\frac{3π}{8}+2kπ}](k∈Z)$ | ||
| C. | $[{\frac{3π}{8}+kπ,\frac{7π}{8}+kπ}](k∈Z)$ | D. | $[{-\frac{π}{8}+kπ,\frac{3π}{8}+kπ}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | i | C. | $\frac{4}{5}-i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | [0,2] | C. | [-2,0] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com