
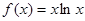 .
.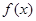 的单调区间和极值;
的单调区间和极值;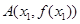 ,
,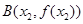 ,且
,且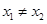 ,证明:
,证明: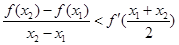 .
. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
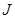 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,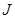 型卡车满载行驶时,每100km所消耗的燃油量
型卡车满载行驶时,每100km所消耗的燃油量 (单位:
(单位: )与速度
)与速度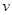 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.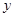 (元)(不计返程费用),将
(元)(不计返程费用),将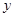 表示成速度
表示成速度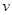 的函数关系式;
的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
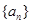 的前
的前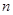 项和为
项和为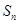 ,对一切正整数
,对一切正整数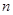 ,点
,点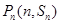 都在函数
都在函数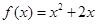 的图像上,且过点
的图像上,且过点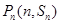 的切线的斜率为
的切线的斜率为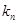 .
.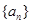 的通项公式;
的通项公式;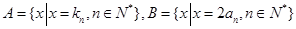 ,等差数列
,等差数列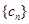 的任一项
的任一项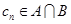 ,其中
,其中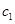 是
是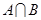 中所有元素的最小数,
中所有元素的最小数,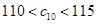 ,求
,求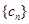 的通项公式.
的通项公式.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
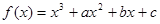 ,在定义域
,在定义域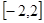 上表示的曲线过原点,且在
上表示的曲线过原点,且在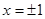 处的切线斜率均为
处的切线斜率均为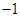 .有以下命题:
.有以下命题: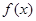 是奇函数;②若
是奇函数;②若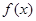 在
在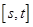 内递减,则
内递减,则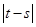 的最大值为4;③
的最大值为4;③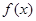 的最大值为
的最大值为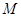 ,最小值为
,最小值为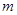 ,则
,则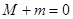 ; ④若对
; ④若对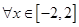 ,
,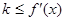 恒成立,则
恒成立,则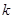 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com