
【题目】已知多面体![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形, ![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求
,求![]() 的值.
的值.
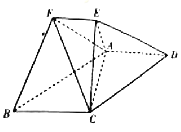
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先由线面垂直![]() 平面
平面![]() 性质定理得
性质定理得![]() ,再利用计算,根据勾股定理得
,再利用计算,根据勾股定理得![]() ,利用线面垂直判定定理得
,利用线面垂直判定定理得![]() 平面
平面![]() .最后根据面面垂直判定定理得平面
.最后根据面面垂直判定定理得平面![]() 平面
平面![]() .(2)研究线面角,可利用空间向量进行列式求解参数,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求解参数.
.(2)研究线面角,可利用空间向量进行列式求解参数,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求解参数.
试题解析:(Ⅰ)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为原点,
为原点, ![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() 轴,过点
轴,过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() (
(![]() ),则
),则![]() ,
, ![]() ,
, 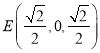 ,
, 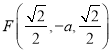 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,因为
,因为![]() ,
, 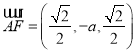 ,
,
所以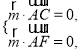 即
即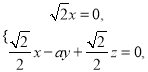 取
取![]() ,得
,得![]() ,则
,则![]() .
.
又因为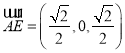 ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则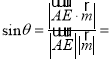
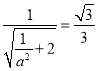 ,
,
解得![]() (
(![]() 舍去),故
舍去),故![]() .
.


科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,试判断函数f(x)零点个数;
(2)若对x1x2∈R,且x1<x2 , f(x1)≠f(x2),证明方程f(x)= ![]() 必有一个实数根属于(x1 , x2).
必有一个实数根属于(x1 , x2).
(3)是否存在a,b,c∈R,使f(x)同时满足以下条件
①当x=﹣1时,函数f(x)有最小值0;
②对任意x∈R,都有0≤f(x)﹣x≤ ![]() 若存在,求出a,b,c的值,若不存在,请说明理由.
若存在,求出a,b,c的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
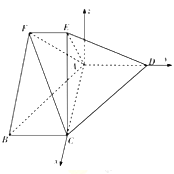
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() ,
, ![]() ,
, ![]() 的平面截该正方体所得的截面为
的平面截该正方体所得的截面为![]() ,则下列命题正确的是__________(写出所有正确命题的编号).
,则下列命题正确的是__________(写出所有正确命题的编号).

①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为五边形;
为五边形;
⑤当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=a﹣bcos(2x+ ![]() )(b>0)的最大值为3,最小值为﹣1.
)(b>0)的最大值为3,最小值为﹣1.
(1)求a,b的值;
(2)当求x∈[ ![]() ,
, ![]() π]时,函数g(x)=4asin(bx﹣
π]时,函数g(x)=4asin(bx﹣ ![]() )的值域.
)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如下图所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;

(Ⅱ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
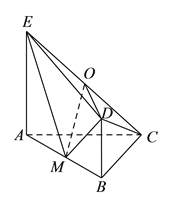
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(I)求证:![]() 平面
平面![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)能否在![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ?若能,请指出点
?若能,请指出点![]() 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com