
【题目】已知函数y=a﹣bcos(2x+ ![]() )(b>0)的最大值为3,最小值为﹣1.
)(b>0)的最大值为3,最小值为﹣1.
(1)求a,b的值;
(2)当求x∈[ ![]() ,
, ![]() π]时,函数g(x)=4asin(bx﹣
π]时,函数g(x)=4asin(bx﹣ ![]() )的值域.
)的值域.
【答案】
(1)解:∵函数y=a﹣bcos(2x+ ![]() )(b>0)的最大值为3,最小值为﹣1,
)(b>0)的最大值为3,最小值为﹣1,
∴ ![]() ,解得
,解得 ![]() .
.
(2)解:由(1)可得函数g(x)=4asin(bx﹣ ![]() )=4sin(2x﹣
)=4sin(2x﹣ ![]() ),
),
∵x∈[ ![]() ,
, ![]() π],∴2x﹣
π],∴2x﹣ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
故函数g(x)的值域为: ![]()
【解析】(1)由题意可得 ![]() ,由此求得a、b的值.(2)由(1)可得函数g(x)=4sin(2x﹣
,由此求得a、b的值.(2)由(1)可得函数g(x)=4sin(2x﹣ ![]() ),根据 x∈[
),根据 x∈[ ![]() ,
, ![]() π],利用正弦函数的定义域和值域求得函数g(x)的值域.
π],利用正弦函数的定义域和值域求得函数g(x)的值域.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 和定点
和定点![]() ,由圆
,由圆![]() 外一点
外一点![]() 向圆
向圆![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.
(1)求实数![]() ,
,![]() 满足的等量关系;
满足的等量关系;
(2)求线段![]() 长的最小值;
长的最小值;
(3)若以![]() 为圆心所作的圆
为圆心所作的圆![]() 与圆
与圆![]() 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() =λ
=λ ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]()
![]() =0.
=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )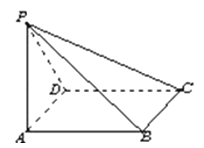
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com