
����Ŀ��Ϊ�˸��õع滮��������������֤�߲˵����ʳ̶ȣ�ij�߲��̵��ijһ������������У������ȡ��8��������Ϊ�о���������ͼ��ʾ��![]() ���֣�Ϊ����߲˵�������
���֣�Ϊ����߲˵������� ![]() ���죩Ϊ������������
���죩Ϊ������������
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
�������ϱ����������������л���ɢ��ͼ��

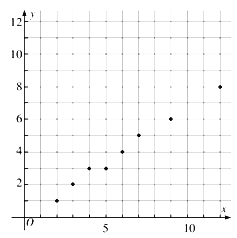
�������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
�����ݣ����еļ������������߲��̵���һ�������25�֣���Ԥ����Ҫ���۶�����.
�ο���ʽ��  ��
�� ![]() .
.
���𰸡���1����������2��![]() ��3������17��.
��3������17��.
�������������������1��������㷨��ɢ��ͼ����2������ƽ����![]() ��
�� ![]() ���ٴ���ʽ
���ٴ���ʽ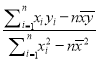 ��
��![]() ������
������![]() ��
��![]() �����ûع�ֱ�߷��̣���3��ʵ�������Ա���Ϊ25ʱ��Ӧ�ĺ���ֵ������
�����ûع�ֱ�߷��̣���3��ʵ�������Ա���Ϊ25ʱ��Ӧ�ĺ���ֵ������![]() ����ع�ֱ�߷��̣��ɵ�Ԥ����Ҫ����17��.
����ع�ֱ�߷��̣��ɵ�Ԥ����Ҫ����17��.
�������������ɢ��ͼ��ͼ��ʾ��
���������⣬ ![]()
![]() ��
�� ![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]() ��
�� ![]() ��
��
![]() �ع�ֱ�߷���Ϊ
�ع�ֱ�߷���Ϊ![]() .
.
�����ɣ���֪����![]() ʱ��
ʱ�� ![]()
![]() .
.
����һ��������߲�25�֣���Ԥ����Ҫ����17��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��1��2����
=��1��2���� ![]() =��2����2����
=��2����2����
��1���� ![]() =4
=4 ![]() +
+ ![]() ����
���� ![]() ��
��
��2���� ![]() +
+ ![]() ��
�� ![]() ��ֱ����˵�ֵ��
��ֱ����˵�ֵ��
��3�������� ![]() ��
�� ![]() �����ϵ�ͶӰ��
�����ϵ�ͶӰ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}������Ϊa������Ϊb������ax2��3x��2=0�Ľ�Ϊ1��b��
(1)������{an}��ͨ�ʽ��
(2)������{bn}����bn��an��2n��������{bn}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���γ���Ϊ���οͽ��ܱ��ص����������������һ���и���ƽ��������º�ƽ��������µ��״�ͼ. ͼ��A���ʾʮ�µ�ƽ���������ԼΪ![]() ��B���ʾ���µ�ƽ���������ԼΪ
��B���ʾ���µ�ƽ���������ԼΪ![]() . ������������ȷ���� �� ��
. ������������ȷ���� �� ��

A. ���µ�ƽ��������¶���![]() ����
����
B. ���µ�ƽ���²��һ�µ�ƽ���²��
C. ���º�ʮһ�µ�ƽ��������»�����ͬ
D. ƽ��������¸���![]() ���·���5��
���·���5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У��ı���
�У��ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ� ![]() ƽ��
ƽ��![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() .
.
������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽǵ�����ֵΪ
���ɵĽǵ�����ֵΪ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() �IJ�������Ϊ:
�IJ�������Ϊ: ![]() ,��ƽ��ֱ������ϵxOy��ԭ��OΪ����,x���������Ϊ����,ȡ��ͬ�ij��ȵ�λ����������ϵ,����C�ļ����귽��Ϊ
,��ƽ��ֱ������ϵxOy��ԭ��OΪ����,x���������Ϊ����,ȡ��ͬ�ij��ȵ�λ����������ϵ,����C�ļ����귽��Ϊ![]() .
.
(1)��ֱ��![]() ������C����ͨ����;
������C����ͨ����;
(2)��ֱ������ϵ��,����B(0,1)��ֱ��![]() �Ĵ���,����ΪH,����
�Ĵ���,����ΪH,����![]() Ϊ����,��H�켣�IJ�������,��ָ���켣��ʾ������.
Ϊ����,��H�켣�IJ�������,��ָ���켣��ʾ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
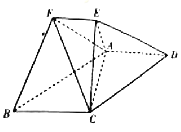
����Ŀ����ͼ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ��������
��������![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ� ![]() ����
����![]() ��
��
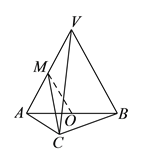
��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ����ֱ��
��Բ����ֱ��![]() �ϣ��ҹ���
�ϣ��ҹ���![]() ����ֱ��
����ֱ��![]() ���У�
����
��![]() ����Բ
����Բ![]() �ķ�����
�ķ�����
��![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣮��ʵ��
���㣮��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��![]() ������
������![]() ���������£��Ƿ����ʵ��
���������£��Ƿ����ʵ��![]() ��ʹ����
��ʹ����![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ����
����![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ֵ���������ڣ���˵��������
��ֵ���������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������S-ABCD�У�����ABCDΪ���Σ�SD��ƽ��ABCD����EΪSD���е㣮
��1����֤��ֱ��SB��ƽ��ACE
��2����֤��ֱ��AC��ƽ��SBD��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com