练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某市一高中二年级在期中考试后进行了研学活动，旅行社推出6条研学路线--A：历史，B：人文，C：诗歌，D：科技，E：政风，F：探秘．
    （Ⅰ）假设每条线路被选中的可能性相同，若从上述6条线路中随机选择4条线路进行研学．求历史与科技两条线路都被选中的概率；
    （Ⅱ）研学结束后，学校从参加研学的所有学生中，随机抽取了100名学生参加对本次研学满意度的调查，满意度得分的统计结果如下表：
    满意度得分[0，50）[50，60）[60，70）[70，80）[80，90）[90，100]
    人数029265211
    试估算学生对本次研学满意度的平均得分．

    分析 （1）使用列举法求出概率；（2）使用组中值代替本组平均分，计算加权平均数．

    解答 解：（1）从6条研学路线随机选择4条的基本事件共有15种，它们分别是（ABCD），（ABCE），（ABCF），（ABDE），（ABDF），（ABEF），（ACDE），（ACDF），（ACEF），（ADEF），（BCDE），
    （BCDF），（BCEF），（BDEF），（CDEF），且它们发生的机会均等．其中历史和科技都被选中的概率共有6种，他们是（ABCD），（ABDE），（ACDE），（ACDF），（ADEF），（ABDF）．
    ∴历史与科技两条线路都被选中的概率为$\frac{6}{15}$=$\frac{2}{5}$．
    （2）$\overline{x}$=$\frac{1}{100}$（55×2+65×9+75×26+85×52+95×11）=81.1
    ∴学生对本次研学满意度的平均得分是81.1．

    点评 本题考查了古典概型的概率计算，用样本估计总体的统计思想，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

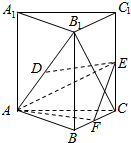    2．已知三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AB=AC，D，E，F分别为B1A，C1C，BC的中点．
    （I）求证：DE∥平面ABC；
    （II）求证：平面AEF⊥平面BCC1B1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知二次函数f（x）=x2-2x-1．
    （1）判断f（x）图象的开口方向、对称轴及单调性．
    （2）解方程f（x）=x-3．
    （3）当x∈[-1，2]时，求函数f（x）的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设双曲线的中心在原点，焦点在x轴上，离心率e为$\sqrt{5}$，则该双曲线的两条渐近线方程为（　　）
    A．y=±2xB．y=±$\frac{1}{2}x$C．y=±4xD．y=±x

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知数列{an}的前n项和为Sn，Sn-2an=1（n∈N*），则数列{an}的通项公式an=2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．把5张分别写有数字1，2，3，4，5的卡片混合，再将其任意排成一行，则得到的数能被2或5整除的概率是（　　）
    A．0.2B．0.4C．0.6D．0.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设log23=t，s=log672，若用含t的式子表示s，则s=$\frac{3+2t}{1+t}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若抛物线C1：y=$\frac{1}{4}$x2的焦点F到双曲线C2：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的距离为$\frac{\sqrt{3}}{2}$，抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$，则双曲线C2的方程为（　　）
    A．$\frac{{x}^{2}}{3}$-y2=1B．x2-$\frac{{y}^{2}}{3}$=1C．$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1D．$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．某市进行一次高三教学质量抽样检测，考试后统计的所有考生的数学成绩服从正态分布．已知数学成绩平均分为90分，60分以下的人数占10%，则数学成绩在90分至120分之间的考生人数所占百分比约为40%．

    查看答案和解析>>

    同步练习册答案