[题目]如图.在直三棱柱ABC﹣A1B1C1中.AB=1.AC=2.BC= .D.E分别是AC1和BB1的中点.则直线DE与平面BB1C1C所成的角为( ) A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AB=1，AC=2，BC= ，D，E分别是AC1和BB1的中点，则直线DE与平面BB1C1C所成的角为（）

A.
B.
C.
D.

【答案】A
【解析】解：取AC的中点为F，连接BF、DF．因为在直三棱柱ABC﹣A1B1C1中，CC1∥BB1 ，又因为DF是三角形ACC1的中位线，故DF= CC1= BB1=BE，故四边形BEDF是平行四边形，所以ED∥BF．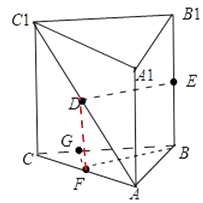

过点F作FG垂直与BC交BC与点G，由题意得∠FBG即为所求的角．
因为AB=1，AC=2，BC= ，所以∠ABC= ，∠BCA= ，直角三角形斜边中线BF是斜边AC的一半，故BF= AC=CF，所以
∠FBG=∠BCA= ．
故选A．
【考点精析】通过灵活运用空间角的异面直线所成的角，掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则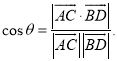即可以解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点．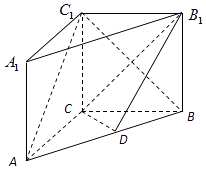

（1）求证：AC⊥BC1；
（2）求证：AC1∥平面CDB1；
（3）求二面角B﹣DC﹣B1的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知曲线上任意一点到直线的距离比到点的距离大1.

（1）求曲线的方程；

（2）过曲线的焦点，且倾斜角为的直线交于点（在轴上方），为的准线，点在上且,求到直线的距离.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图1，2，在Rt△ABC中，AB=BC=4，点E在线段AB上，过点E作交AC于点F，将△AEF沿EF折起到△PEF的位置（点A与P重合），使得∠PEB=60°．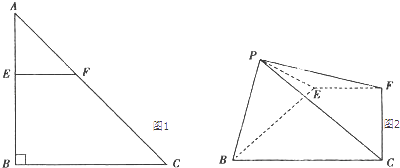

（1）求证：EF⊥PB；
（2）试问：当点E在何处时，四棱锥P﹣EFCB的侧面的面积最大？并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=（）x ，函数g（x）=log x．
（1）若g（ax2+2x+1）的定义域为R，求实数a的取值范围；
（2）当x∈[（）t+1 ，（）t]时，求函数y=[g（x）]2﹣2g（x）+2的最小值h（t）；
（3）是否存在非负实数m，n，使得函数y=log f（x2）的定义域为[m，n]，值域为[2m，2n]，若存在，求出m，n的值；若不存在，则说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，椭圆M： =1（a＞b＞0）的离心率为，直线x=±a和y=±b所围成的矩形ABCD的面积为8．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）设直线l：y=x+m（m∈R）与椭圆M有两个不同的交点P，Q，l与矩形ABCD有两个不同的交点S，T．求的最大值及取得最大值时m的值．

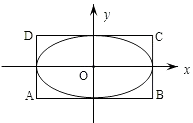
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P（单位：万元）和Q（单位：万元），它们与进货资金t（单位：万元）的关系有经验公式P= t和Q= ．某商场决定投入进货资金50万元，全部用来购入这两种电脑，那么该商场应如何分配进货资金，才能使销售电脑获得的利润y（单位：万元）最大？最大利润是多少万元？