
分析 (Ⅰ)求出函数的导数,计算f′(2),f(2),代入切线方程即可;
(Ⅱ)求出f(x)的单调区间,通过讨论a的范围,得到f(x)在[a,2]的单调性,从而求出函数的最小值即可.
解答 解:(Ⅰ)由题意得:f′(x)=3x2-3x,
∴f′(2)=6,又因为f(2)=3,
所以曲线y=f(x)在在点(2,f(2))处的切线方程为y-3=6(x-2),
即y=6x-9;
(Ⅱ)因为f′(x)=3x2-3x,令f′(x)=0,解得x=0或x=1,
所以f(x)的单增区间为(-∞,0),(1,+∞),
所以f(x)的单减区间为(-∞,0),(1,+∞),
因为a>0所以分两种情况:
①若0<a<1
| x | (a,1) | 1 | [1,2] |
| f′(x) | - | 0 | + |
| f(x) | 单减 | 极小值 | 单增 |
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源:2017届江苏南通市如东县等高三10月联考数学试卷(解析版) 题型:填空题
对于函数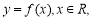 ,“
,“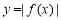 的图象关于y轴对称”是“
的图象关于y轴对称”是“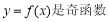 ”的 条件.(填“充分不必要”, “必要不充分”,“充要”,“既不充分也不必要”)
”的 条件.(填“充分不必要”, “必要不充分”,“充要”,“既不充分也不必要”)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤1 | B. | m≤-1 | C. | m>1 | D. | m>-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com