
下列关于命题的说法中正确的是________.
①对于命题p:∃x∈R,使得x2+x+1<0,则綈p:∀x∈R,均有x2+x+1≥0
②“x=1”是“x2-3x+2=0”的充分不必要条件
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
④若p∧q为假命题,则p,q均为假命题
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
对于E={a1,a2,…,a100}的子集X={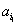 ,
, ,…,
,…,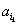 },定义X的“特征数列”为x1,x2,…,x100,其中
},定义X的“特征数列”为x1,x2,…,x100,其中 =
=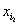 =…=
=…= =1,其余项均为0.例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.
=1,其余项均为0.例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.
(1)子集{a1,a3,a5}的“特征数列”的前3项和为________;
(2)若E的子集P的“特征数列”p1,p2,…,p100满足p1=1,pi+pi+1=1,1≤i≤99;E的子集Q的“特征数列”q1,q2,…,q100满足q1=1,qj+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于原命题“单调函数不是周期函数”,下列陈述正确的是________.
①逆命题为“周期函数不是单调函数”
②否命题为“单调函数是周期函数”
③逆否命题为“周期函数是单调函数”
④以上三者都不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
若有穷数列 ,
,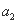 ,
, ,
, (
(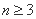 )满足:(1)
)满足:(1) ;(2)
;(2)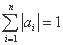 .
.
则称该数列为“ 阶非凡数列”.
阶非凡数列”.
(Ⅰ)分别写出一个单调递增的“ 阶非凡数列”和一个单调递减的“
阶非凡数列”和一个单调递减的“ 阶非凡数列”;
阶非凡数列”;
(Ⅱ)设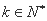 ,若“
,若“ 阶非凡数列”是等差数列,求其通项公式;
阶非凡数列”是等差数列,求其通项公式;
(Ⅲ)记“ 阶非凡数列”的前
阶非凡数列”的前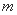 项的和为
项的和为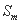 (
(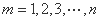 ),证明:
),证明:
(1)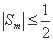 ; (2)
; (2) .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com